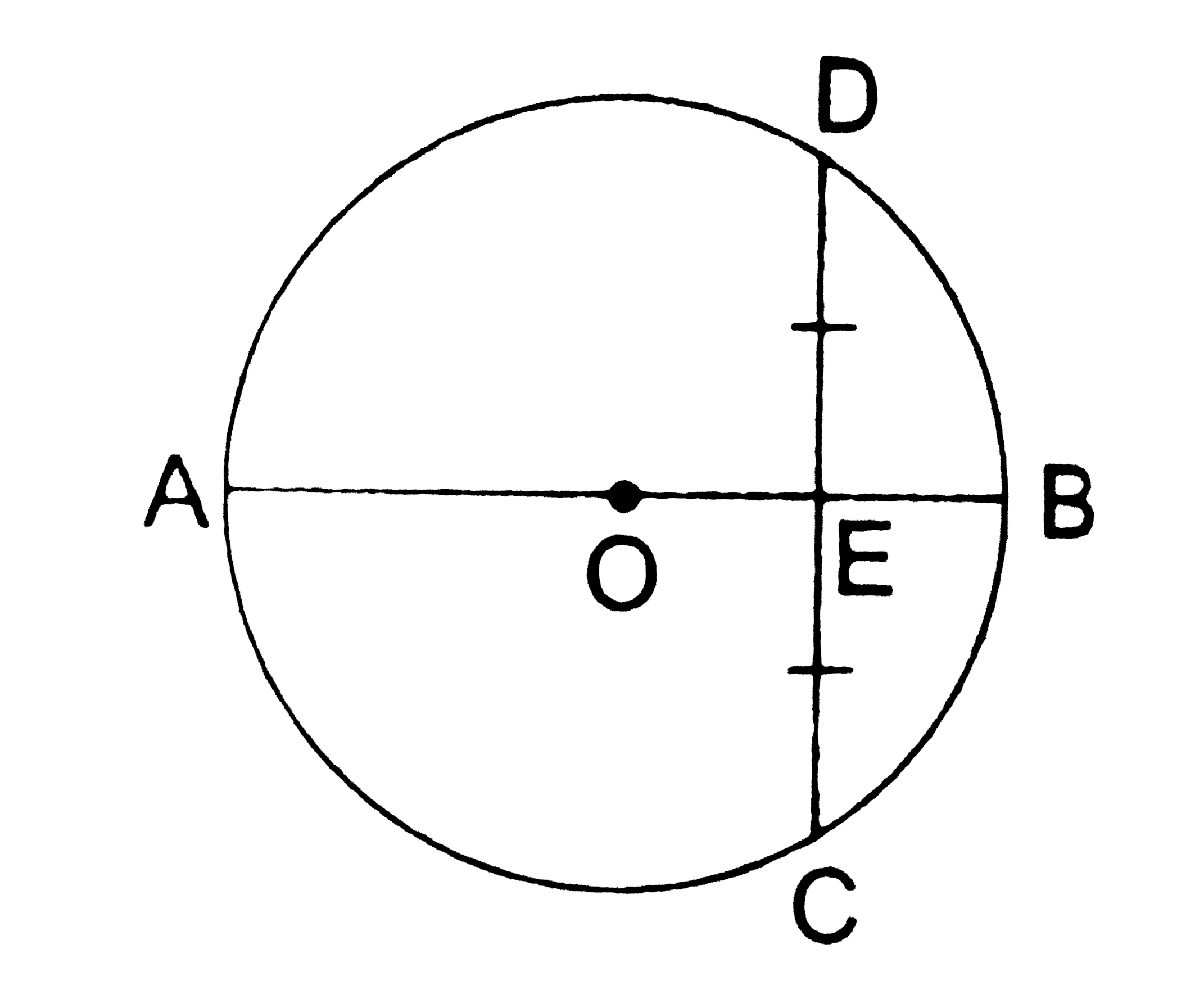
In the given figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = CD = 8cm and EB = 4cm. The radius of the circle is
10cm
12cm
6cm
8cm
The correct Answer is:A
Let the radius of the circle be r cm.
Then, OD=OB=rcm,OE=(r−4)cm,ED=8cm.
Now, OD2=OE2+ED2⇒r2=(r−4)+82
∴8r=80⇒r=10cm
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of a circle of radius 13 cm and AB is a chord perpendicular to OD. If CD = 8 cm, then what is the length (in cm) of AB?
 AA)6 cmBB)12 cmCC)24 cmDD)28cm
AA)6 cmBB)12 cmCC)24 cmDD)28cmIn the given figure, O is the centre of the circle. Radius of the circle is 17 cm. lf OC=8cm, then the length of the chord AB is :
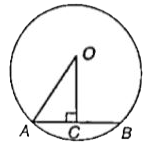 A35 cmB30 cmC15 cmD18 cm
A35 cmB30 cmC15 cmD18 cm
In the given figure, a straight line l passing through the centre O of the circle bisects the chord AB and CD. Prove that AB||CD.
View SolutionIn the given figure, O is the centre of a circle such that OA = 5 cm, AB = 8 cm and OD⊥AB meeting AB at C. Find the length of CD.
View SolutionIn the given fig, AB is the diameter of the circle with centre O. The point C, D and E are on the circle such that AC = CD = DE = EB. Find ∠EBA.
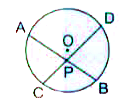
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point P within the circle. If AB = 18 cm, PB = 8 cm, CP = 5 cm, then find the length of CD.
View SolutionIn the figure (i) given below, O is the centre of the circle. AB and CD are the chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB=24 cm OM=5 cm, ON=12 cm. Find the, (i) radius of the circle (ii) length of chord CD (ii) In the figure (ii) given below, CD is diameter which meets the chord AB at E such that AE = BE = 4 cm.If CE = 3 cm, find the radius of the circle.
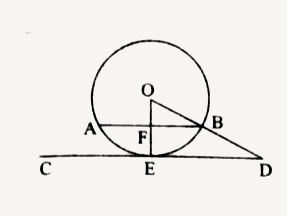
View SolutionIn the figure above, O is the centre of the circle CD is a tangent to the circle at E. OE bisects the chord AB at F. AB = 16 cm and EF = 2 cm. Find the length of DE (in cm).
View Solution