Two circles intersect each other at point P an Q. If PA and PB are two diameter then find ∠AQB.
120∘
135∘
160∘
180∘
To find the angle ∠AQB formed by the intersection of two circles at points P and Q with diameters PA and PB, we can follow these steps:
1. Understanding the Setup:
- We have two circles intersecting at points P and Q.
- PA and PB are diameters of the two circles.
2. Identifying Key Angles:
- Since PA is a diameter of the first circle, the angle AQP (formed by points A, Q, and P) is inscribed in a semicircle. By the inscribed angle theorem, this angle is 90∘.
- Similarly, since PB is a diameter of the second circle, the angle BQP (formed by points B, Q, and P) is also inscribed in a semicircle, making this angle 90∘ as well.
3. Calculating ∠AQB:
- Now, we can find ∠AQB by adding the two angles we found:
∠AQB=∠AQP+∠BQP=90∘+90∘=180∘
4. Conclusion:
- Therefore, the angle ∠AQB is 180∘.
Final Answer:
∠AQB=180∘
- We have two circles intersecting at points P and Q.
- PA and PB are diameters of the two circles.
- Since PA is a diameter of the first circle, the angle AQP (formed by points A, Q, and P) is inscribed in a semicircle. By the inscribed angle theorem, this angle is 90∘.
- Similarly, since PB is a diameter of the second circle, the angle BQP (formed by points B, Q, and P) is also inscribed in a semicircle, making this angle 90∘ as well.
- Now, we can find ∠AQB by adding the two angles we found:
∠AQB=∠AQP+∠BQP=90∘+90∘=180∘
- Therefore, the angle ∠AQB is 180∘.
∠AQB=180∘
Topper's Solved these Questions
Similar Questions
In the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.

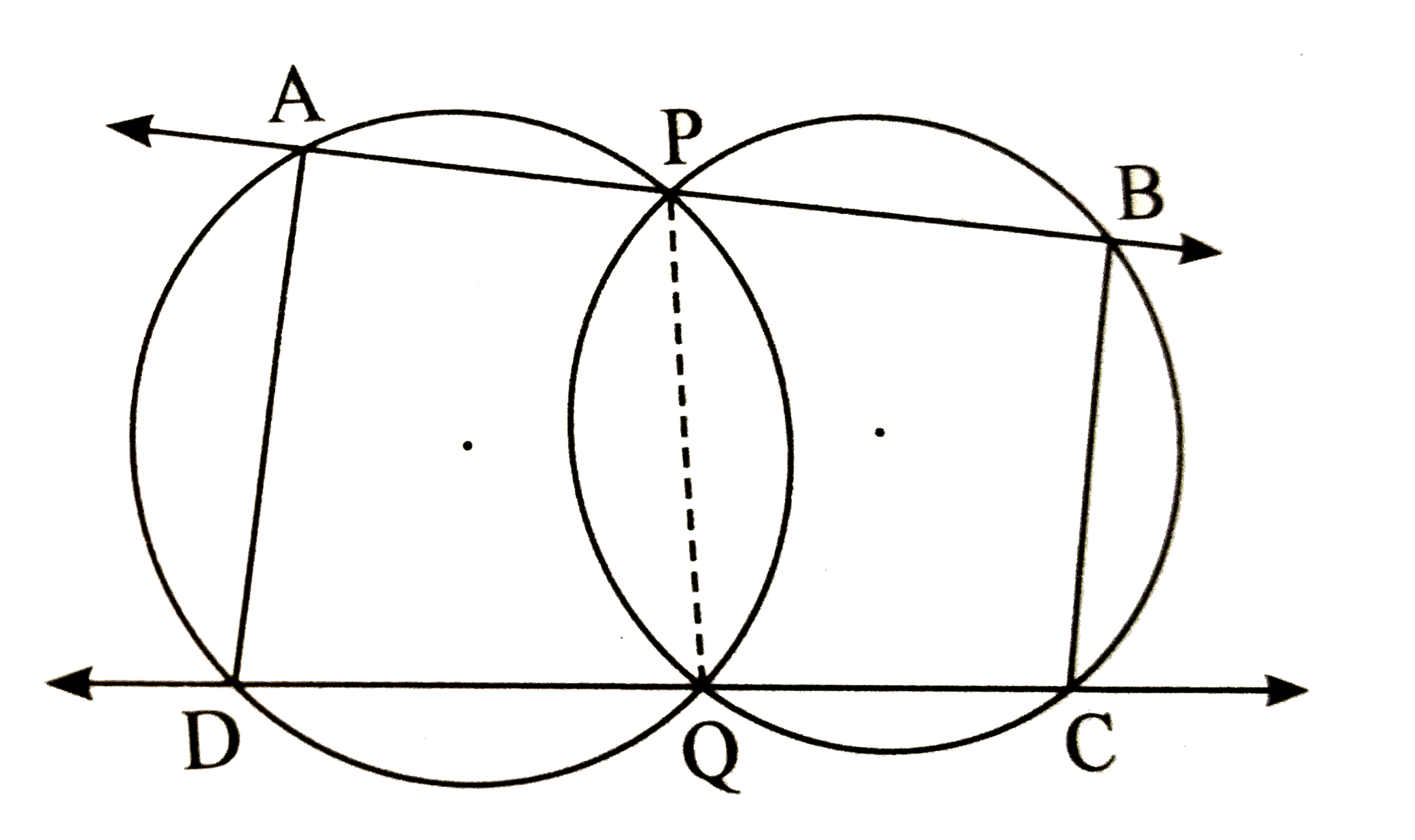
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
View Solution
Knowledge Check
Two circles intersect each other at P and Q. PA and PB are two diameters. Then ∠AQB is
A120∘B135∘C160∘D180∘
As per the figure, two circles intersect each other at points P and Q. Point A is on PQ produced and AMD and ASR are the secants to the circles. If AM = 3, MD = 5, AS = 4, The value of SR is :
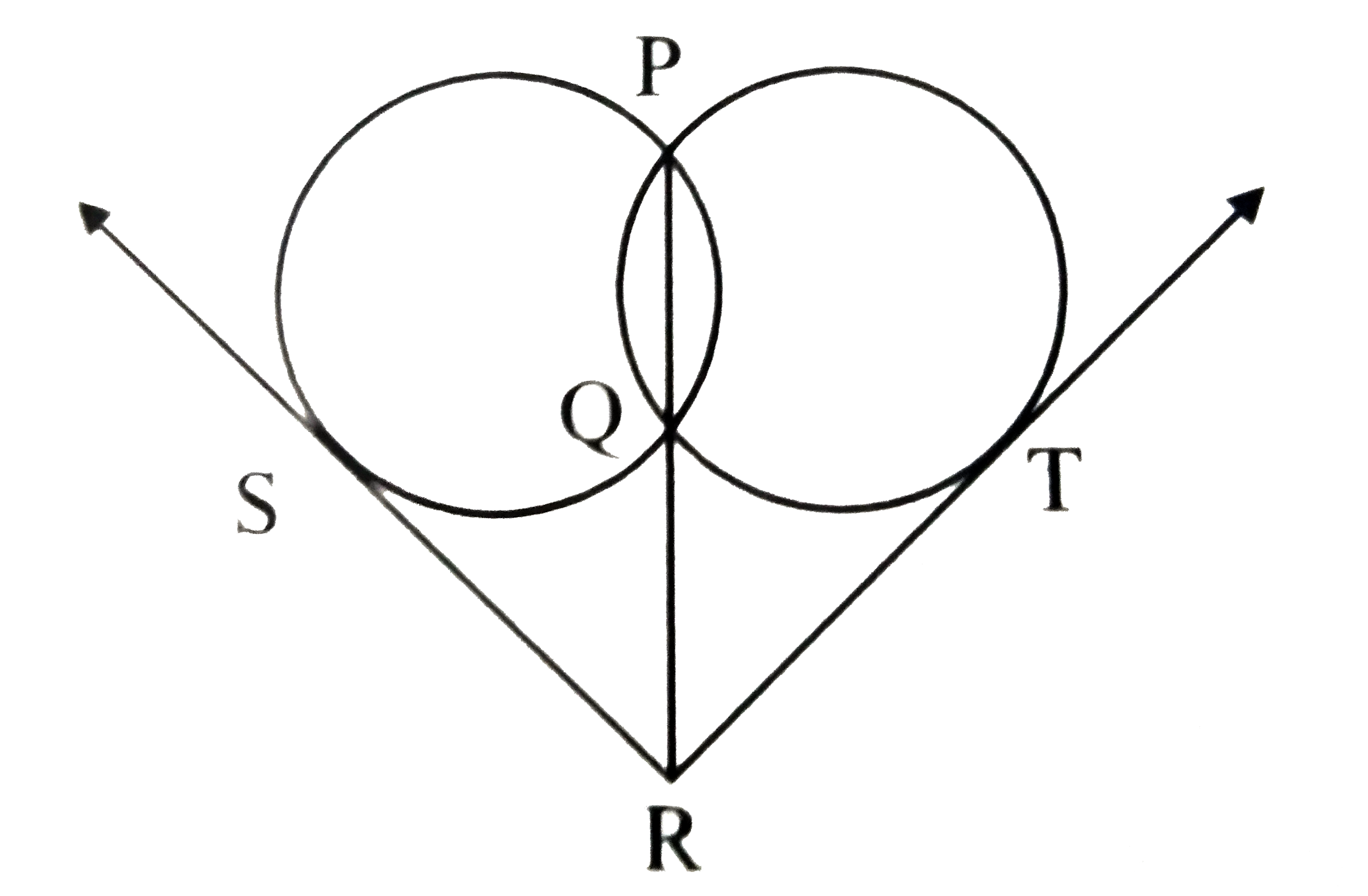
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
View SolutionIn figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.

View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
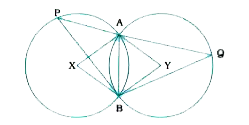
View SolutionTwo congruent circles intersect each other at points A and B. Through A any line segment PAS is drawn so that P, Olie on the two circles. Prove that BP = BQ.
View SolutionIn figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.

View SolutionIn the fig. two circles intersect each other in point A and B. Secants through the point A intersect the circles in point P,Q and R,S. Line PR and SQ intersect in T. (i) PTQ and PBQ are supplementary. (ii) □ BSTR is cyclic quadrilateral.
View Solution
