Two circles intersect each other at P and Q. PA and PB are two diameters. Then ∠AQB is
120∘
135∘
160∘
180∘
The correct Answer is:D
To solve the problem, we need to find the angle ∠AQB formed by the intersection of two circles at points P and Q, where PA and PB are diameters of the respective circles.
1. Understanding the Setup:
- We have two circles that intersect at points P and Q.
- PA and PB are diameters of the two circles.
2. Drawing the Circles:
- Draw two circles that intersect at points P and Q.
- Mark the points A and B on the circles such that PA and PB are diameters.
3. Identifying Angles:
- According to the properties of circles, the angle subtended by a diameter at any point on the circumference is a right angle (90 degrees).
- Therefore, ∠AQP=90∘ and ∠BQP=90∘.
4. Using the Angles:
- Since both ∠AQP and ∠BQP are right angles, we can express the angle ∠AQB as the sum of these two angles:
∠AQB=∠AQP+∠BQP=90∘+90∘=180∘
5. Conclusion:
- Thus, the measure of angle ∠AQB is 180∘.
Final Answer:
The angle ∠AQB is 180∘.
- We have two circles that intersect at points P and Q.
- PA and PB are diameters of the two circles.
- Draw two circles that intersect at points P and Q.
- Mark the points A and B on the circles such that PA and PB are diameters.
- According to the properties of circles, the angle subtended by a diameter at any point on the circumference is a right angle (90 degrees).
- Therefore, ∠AQP=90∘ and ∠BQP=90∘.
- Since both ∠AQP and ∠BQP are right angles, we can express the angle ∠AQB as the sum of these two angles:
∠AQB=∠AQP+∠BQP=90∘+90∘=180∘
- Thus, the measure of angle ∠AQB is 180∘.
The angle ∠AQB is 180∘.
Similar Questions
Knowledge Check
In the given figure, two circles with their respective centres intersect each other at A and B and AB intersects OO at M, then m ∠OMA is:
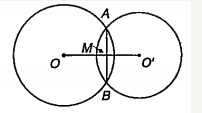 A60∘B80∘C90∘Dcan't be determined
A60∘B80∘C90∘Dcan't be determinedThree circles each of units radius intersects each other at P,QandR.P,QandR are the centres of the three circles. What is the sum of length of the arcs PQ,QRandPR ?
A√3πB2√2πCπDnone of theseThree circles each of units radius intersects each other at P,QandR.P,QandR are the centres of the three circles. What is the sum of length of the arcs PQ,QRandPR ?
A√3πB2√2πCπDnone of these
In the given figure, two circles with their respective centres intersect each other at A and B and AB intersects OO at M, then m ∠OMA is:

View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
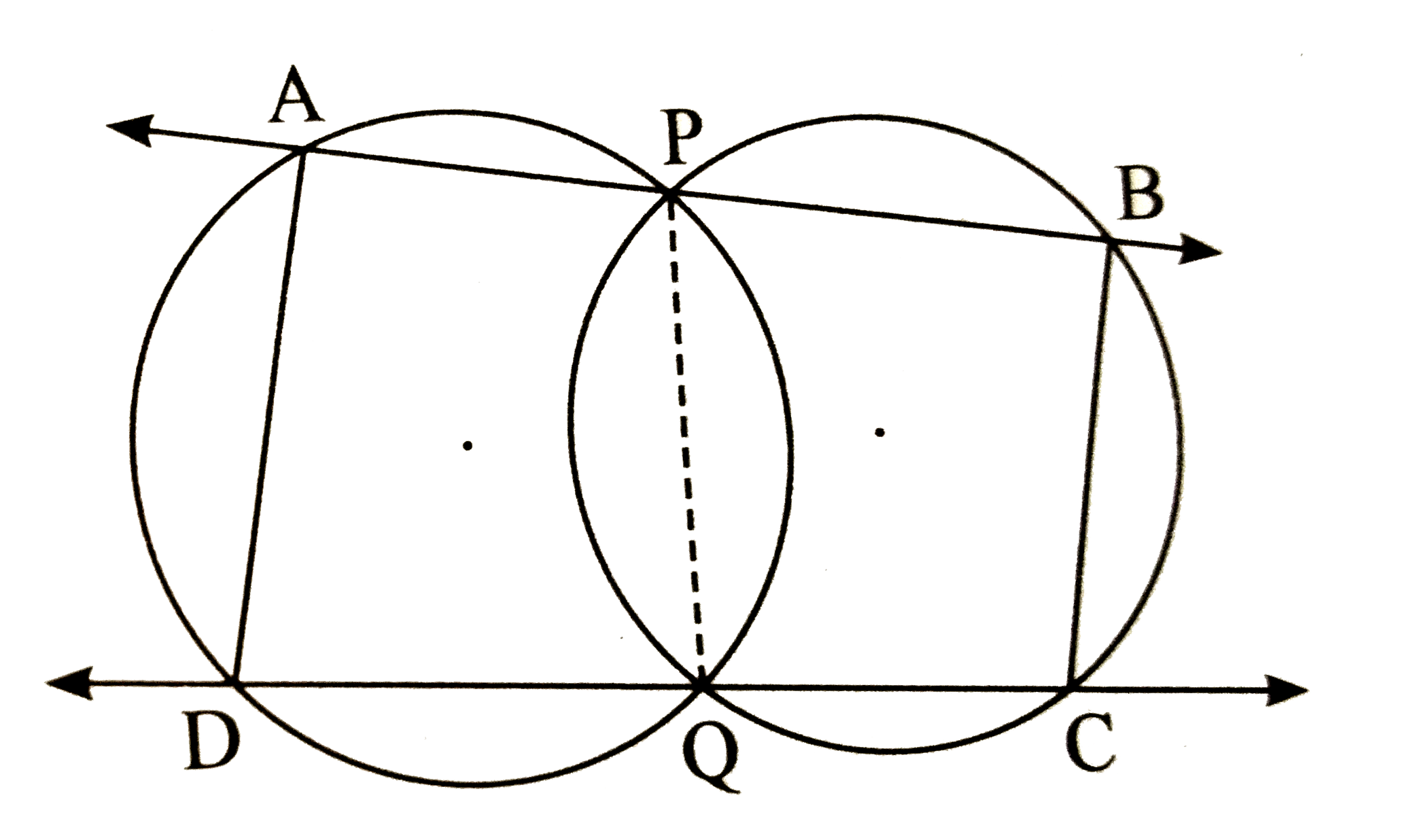
View SolutionAs per the figure, two circles intersect each other at points P and Q. Point A is on PQ produced and AMD and ASR are the secants to the circles. If AM = 3, MD = 5, AS = 4, The value of SR is :
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P, If ∠AOB=15∘and∠APB=30∘, then ∠COD is equal to
View Solution

