Question

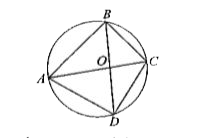
O is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P, If $\angle AOB={15}^{\circ }\text{and}\angle APB={30}^{\circ },$ then $\angle COD$ is equal to

Answer

C

Explanation

To solve the problem, we need to find the value of angle COD given the angles AOB and APB. Let's break it down step by step.

1. Identify the Given Angles:
- We have angle AOB = 15°.
- We have angle APB = 30°.

2. Use the Angle Relationship:
- According to the properties of intersecting chords in a circle, the following relationship holds:
\( \text{Angle AOB} + \text{Angle COD} = 2 \times \text{Angle APB} \)
- This means that:
\( 15° + \text{Angle COD} = 2 \times 30° \)

3. Calculate the Right Side:
- Calculate \(2 \times 30°\):
\( 2 \times 30° = 60° \)

4. Set Up the Equation:
- Now we can set up the equation:
\( 15° + \text{Angle COD} = 60° \)

5. Solve for Angle COD:
- To find Angle COD, subtract 15° from both sides:
\( \text{Angle COD} = 60° - 15° \)
- Therefore:
\( \text{Angle COD} = 45° \)

Final Answer:
Angle COD is equal to 45°.

---