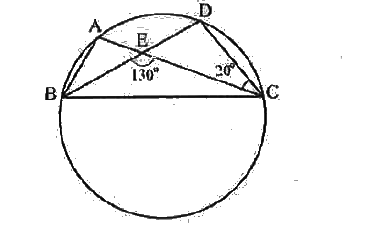
In Fig, A, B, C and D are four points on a circle AC and BD intersect at a point E such that BEC=130∘andECD=20∘. Find BAC.
90∘
100∘
110∘
120∘
The correct Answer is:C
Step by step video, text & image solution for In Fig, A, B, C and D are four points on a circle AC and BD intersect at a point E such that BEC=130^@ and ECD=20^@. Find BAC. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2
100 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
A, B, C, D are four points on a circle. AC and BD intersect at a point E such that ∠BEC=130∘and∠ECD=20∘.∠BAC is
A(A) 120B(B)90∘C(C)100∘D(D)110∘
In fig. 10, A,B,C and D are four points, and no three points are collinear. AC and BD intersect at O. there are eight triangle that you can observe. Name all the triangles.
View SolutionIn triangle ABC, points D and E are on BC and AC respectively. If AD and BE intersect at point F so that AF : FD = 4 : 1 and BD : DC = 2 : 1, than find the ratio BF : BE?
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View Solutiondiagonal of a cocyclic parallelogram ABCD is AC and BD intersection at point R. then
View SolutionThe points A,B,C,D,E are marked on the circumference of a circle in clockwishdirection such that ?ABC=130∘and∠CDE=110∘. The measure of ∠ACE degress is
View SolutionIn triangle ΔABD,∠ADB=20∘ and C is a point on BD such that AB = AC and CD = CA. Find ∠ABC.
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View Solution
