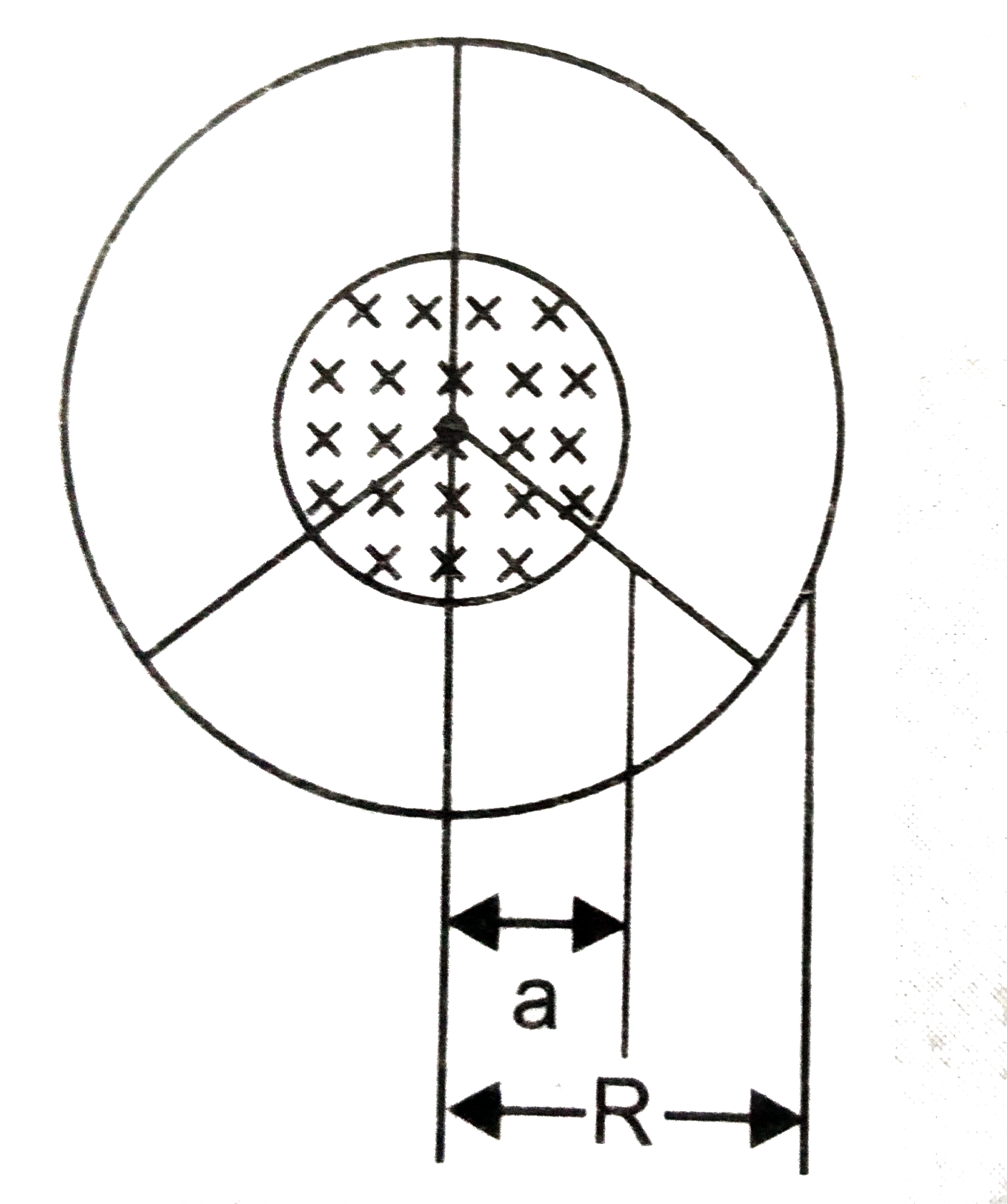
A line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light nonconducting spokes and is free to rotate without friction about its axis as per figure. A uniform magnetic field extends over a circular region within the rim. It is given by,
B=−B0k(r≤a,a<R)
=0 (otherwise)
What is the angular velocity of the wheel after the field is suddenly switched off ?Solution in Gujrati
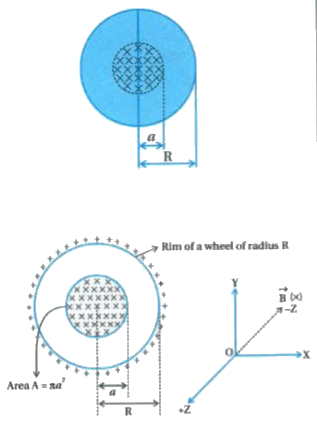
Magnetic flux linked with area A=πa2 of a circle, concentric with given rim of a wheel is,
ϕ=ABcos0∘(∵→A∣∣→B)
∴ϕ=(πa2)B⇒−dϕdt=πa2(−dBdt)…(1)
Here as per the statement when magnetic field is suddenly switch off, above magnetic flux becomes zero. Because of this change in flux, emf is induced in the conducting rim of a wheel in a clockwise direction to increase the flux. This induced emf produces induced electric field given by,
ε=∮→E.→dl
∴ε=∮Edlcos0∘
=E∮dl
∴ε=E(2πR)
∴−dϕdt=E(2πR)
∴πa2(−dBdt)=E(2πR) [From equation (1)]
∴E=a22R(−dBdt)...(2)
Here induced electric field exerts electric force dF on charge dq=λdl (where λ = linear charge = density on the rim of a wheel). Because of this tangential force, torque is exerted on dl length given by,
dtau=(R)(dF)
∴dtau=(R)(dq)E
∴dtau=(R)(λdl)E
∴∫dtau=RλE∫dl
∴τ=RλE(2πR)=2πR2λE
∴Iα=2πR2λ×a22R(−dBdt) [From equation (2)]
∴MR2(dωdt)=πRλa2(−dBdt) (∵I=MR2)
∴dω=−πλa2MRdB
∴∫ωfωidω=−πλa2MR∫BfBidB
∴(ωf−ωi)=−πλa2MR(Bf−Bi)
∴ωf=−πλa2MR(0−B0) (∵ωi=0,Bi=B0 and Bf=0 )
∴ωf=πλa2B0MR
(In the direction , perpendicularly inside the plane of figure , so as to increase inward flux , according to Lenz.s law).
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section B (Numerical) Numerical From DARPAN Based on Textbook
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section C Ncert Exemplar Solution (MCQs)
16 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section B (Numerical) Textual Illustrations
26 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
14 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
Similar Questions
A conducting circular loop is placed in a uniform magnetic field of 0.04 T with its plane perpendicular to the field. Some how, the radius of the loop starts shrinking at a constant rate of 2 mm/s. Find the induced emf in the loop at an instant when the radius becomes 2 cm solution.
View SolutionA square of side L meters lies in the xy-plane in a region, where the magnetic field is given by →B=B0(2ˆi+3ˆj+4ˆk)T where B0 is constant. The magnitude of flux passing through the square is
View Solution
Consider Experiment:
(a) What would you do to obtain a large deflection of the galvanometer ?
(b) How would you demonstrate the presence of an induced current in the absence of a galvanometer ?
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.
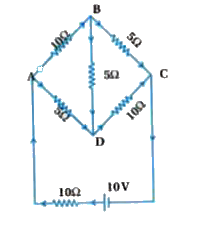
View SolutionA wheel with 4 spokes is placed with its plane perpendicular to a uniform magnetic field B of magnitude 0.5 T. The field is directed into the plane of the paper and is present over the entire region of the wheel as shown in Fig. When the switch S is closed, there is initial current of 6 A between the axis and the rim and the wheel begins to rotate. Resistances of the spokes are 1, 2, 4 and 8 Omega , respectively. Resistance of rim is negligible. a. What is the direction of rotation of the wheel? b. Radius of the wheel is 0.2 m. Calculate initial torque acting on the wheel.
View SolutionA metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity omega in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)
View SolutionA line charge lambda per unit length is pasted uniformly on to the wire of a wheel of mass m and radius R . The wheel has light non-conducting spokes and is free to rotate about a vertical axis as shown in Fig. 3.166 . A uniform magnetic field extends over a radial rigion of radius r given by B = -B_(0)hat(k)(r le a, alt R) = 0 (otherwise). What is the angular velocity of the wheel this field is suddenly switched off?
View SolutionA circular wheel is rotating in horizontal plane without friction about its axis. If a body is gently attached to the rim of the wheel then following is false.
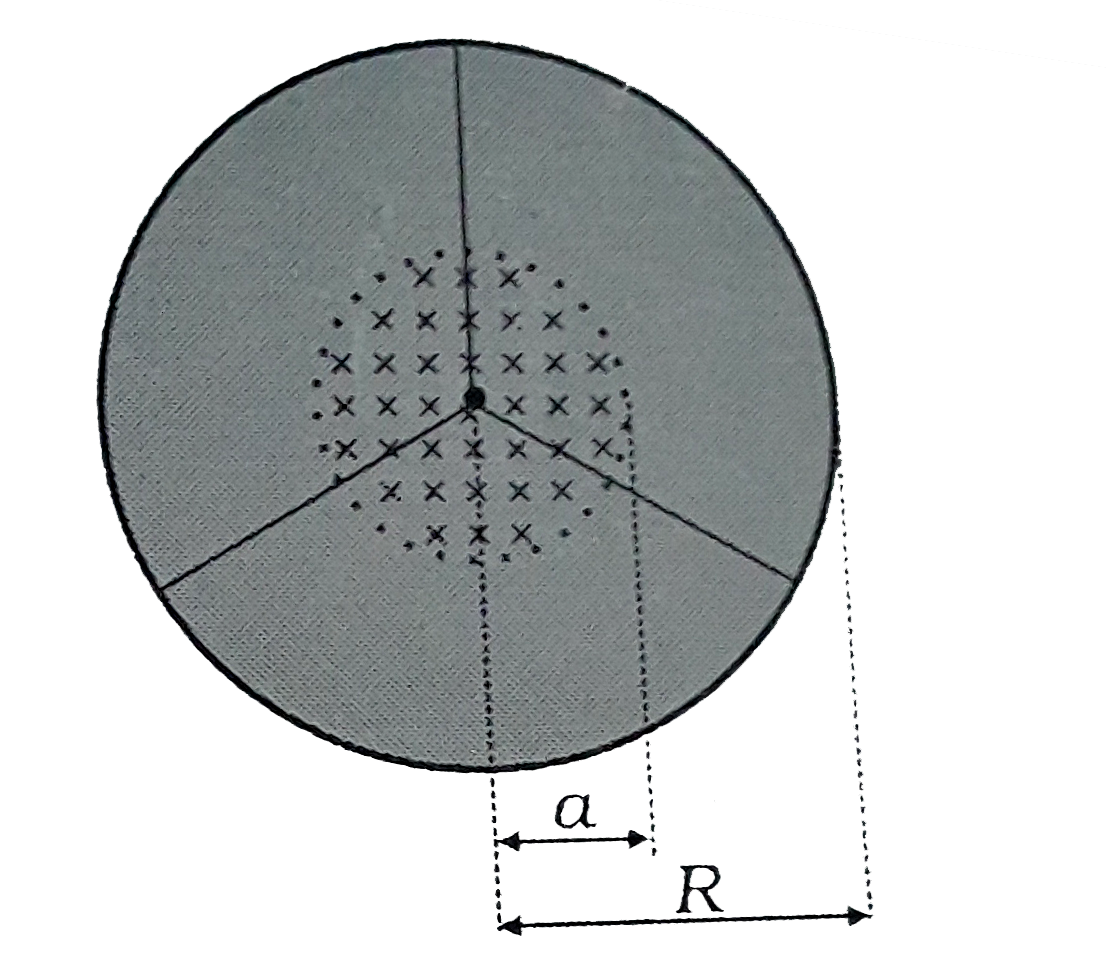
View SolutionA line charge lambda per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig.). A uniform magnetic field extends over a circular region within the rim. It is given by, B=-B_(0)k" "(r le a,a lt R) =0 " " (otherwise) What is the angular velocity of the wheel after the field is suddenly switched off?
View Solutionकिसी M द्रव्यमान तथा R त्रिज्या वाले एक पहिए के किनारे (rim) पर एक रैखिक आवेश स्थापित किया गया है जिसकी प्रति इकाई लंबाई पर आवेश का मान λ है| पहिए के स्पोक (slope) हल्के एवं कुचालक है तथा वह अपनी अक्ष के परित: घूर्णन रहित हेतु स्वतंत्र है जैसा कि चित्र 6.22 में दर्शाया गया है | पहिए के वृतीय भाग पर, रिम के अंदर एकसमान चुंबकीय क्षेत्र विस्तरित है | इसे इस प्रकार परिभाषित किया गया है, B=−B0K (r≤a,a<R)
=0 (अन्यथा)
चुंबकीय क्षेत्र को अचानक 'आफ' (switched off) करने के पश्चात, पहिए का कोणीय वेग ज्ञात कीजिए |
View Solutionकिसी M द्रव्यमान तथा R त्रिज्या वाले एक पहिए कि किनारे (rim) पर एक रैखिक आवेश स्थापित किया गया है जिसकी प्रति इकाई लम्बाई पर आवेश का मान λ है । पहिए के स्पोक (slope) हलके एवं कुचालक है तथा वह अपनी अक्ष के परितः घर्षण रहित घूर्णन हेतु स्वतन्त्र है जैसाकि चित्र में दर्शाया गया है पहिए के वृत्तियाँ भाग पर रिम के अंदर एकसमान चुम्बकीय क्षेत्र विस्तारित है इसे निम्न प्रकार परिभाषित किया गया है ।
B=−B0ˆk(r≤a,a<R)
= 0 (अन्यथा)
चुम्बकीय क्षेत्र को अचानक 'ऑफ़' (switched off) करने के पश्चात पहिए का कोणीय वेग ज्ञात कीजिए ?
View Solutionकिसी M द्रव्यमान तथा R त्रिज्या वाले एक पहिये के किनारे पर रैखिक आवेश स्थापित किया गया है जिसकी प्रति इकाई लम्बाई पर आवेश का मानλ है । पहिये के स्पोक हलके एवं कुचालक है तथा वह अपनी अक्ष के परितः घर्षण रहित घूर्णन हेतु स्वतंत्र है जैसा की चित्र में दर्शाया गया है । पहिए के वृतीय भाग पर , रिम के अंदर एकसमान चुम्बकीय क्षेत्र विस्तरित है । इसे इस प्रकार परिभाषित किया गया है ,
B=−B0k
= 0
( अन्यथा ) चुम्बकीय क्षेत्र को अचानक ( ऑफ ) करने के पश्चात , पहिए का कोणीय वेग ज्ञात कीजिए ।

View SolutionA line charge lambda per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig.) . A uniform magnetic field extends over a circular region within the rim. It is given by, {:(B=-B_0 K,(r le a , a lt R)),(=0,"(otherwise)"):}
View SolutionA line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light nonconducting spokes and is free to rotate without friction about its axis as per figure. A uniform magnetic field extends over a circular region within the rim. It is given by,
B=−B0k(r≤a,a<R)
=0 (otherwise)
What is the angular velocity of the wheel after the field is suddenly switched off ?
View Solution
