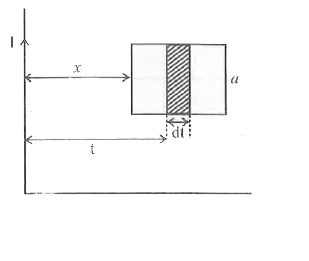
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s. Calculate the induced emf in the loop at the instant when x = 0.2 m. Take a = 0.1 m and assume that the loop has a large resistance.Solution in Gujrati
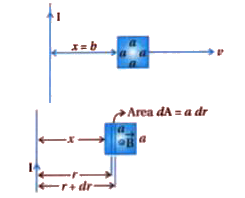
Consider area element in the form of rectangular strip with area dA = a dr at distance r from current carrying extremely long straight wire. Magnetic field through this element is perpendicularly inside the plane of figure. Since the width of above strip is extremely small, magnetic field B=μ0I2πr can be taken almost constant. 2nr Hence, magnetic flux linked with this strip is,
dϕ=BdA
∴dϕ=(μ0I2πr)(adr)
∫Φ0dϕ=μ0Ia2π∫x+ax1rdr
∴{ϕ}Φ0=μ0Ia2π{lnr}x+ax
∴{Φ−0}=μ0Ia2π{ln(x+a)−ln(x)}
∴Φ=μ0Ia2πln(x+ax)
∴Φ=μ0Ia2πln(1+ax)...(1)
Mutual inductance of given system will be ,
M=ΦI=μ0a2πln(1+ax)
(b) Now, when above loop moves with constant velocity v towards right, magnetic flux linked with it goes on decreasing with time.
When loop is at distance x from the wire at time t, emf induced in it will be ,
ε=−dΦdt
∴ε=−(dΦdx)(dxdt)
∴ε=−vdΦdx ( ∵dxdt=v= velocity of loop )
=−vddx{μ0Ia2πln(1+ax)}
=−vμ0Ia2π11+axddx(1+ax)
=−vμ0Ia2π(xx+a){0+addx(1x)}
=−vμ0Ia2π(xx+a){a(−1x2)}
∴ε=μ0Ia2v2πx(x+a)
∴ε=(4π×10−7)(50)(0.1)2(10)(2π)(0.2)(0.2+0.1)
∴ε=1.667×10−5 V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section B (Numerical) Numerical From DARPAN Based on Textbook
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section C Ncert Exemplar Solution (MCQs)
Explore 16 Videos
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section B (Numerical) Textual Illustrations
Explore 26 Videos
- ELECTRIC CHARGES AND FIELDS Book:KUMAR PRAKASHANChapter:ELECTRIC CHARGES AND FIELDS Exercise:SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
Explore 14 Videos
- ELECTROMAGNETIC WAVESBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC WAVESExercise:BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
Explore 5 Videos
Similar Questions
A conducting circular loop is placed in a uniform magnetic field of 0.04 T with its plane perpendicular to the field. Some how, the radius of the loop starts shrinking at a constant rate of 2 mm/s. Find the induced emf in the loop at an instant when the radius becomes 2 cm solution.
View SolutionA square of side L meters lies in the xy-plane in a region, where the magnetic field is given by →B=B0(2ˆi+3ˆj+4ˆk)T where B0 is constant. The magnitude of flux passing through the square is
View Solution
Consider Experiment:
(a) What would you do to obtain a large deflection of the galvanometer ?
(b) How would you demonstrate the presence of an induced current in the absence of a galvanometer ?
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.

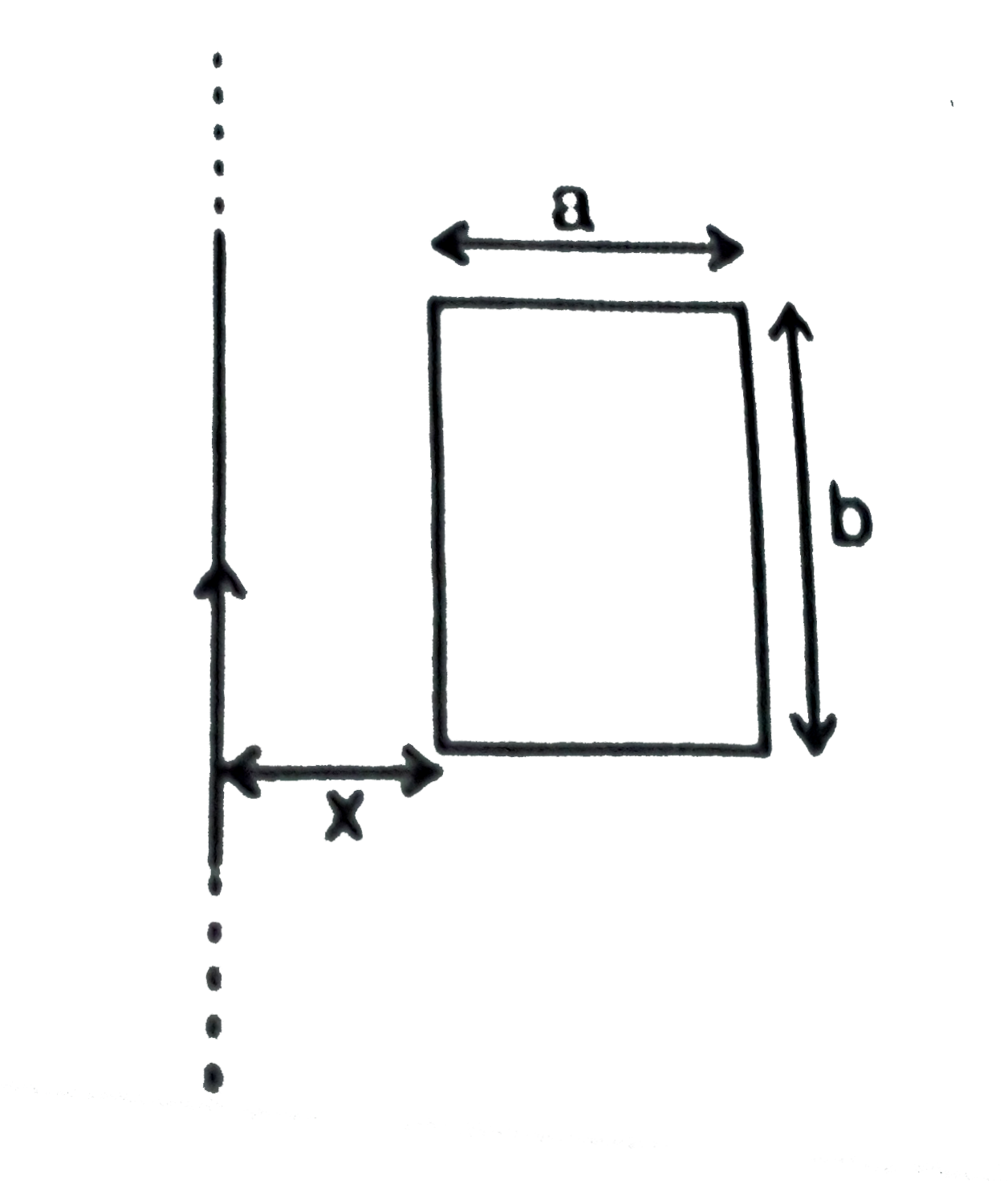
View Solution(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in Fig. (b) Evaluate the induced emf in loop if the wire carries a current of 50 A and the loop has an instantaneous velocity upsilon = 10 ms^(-1) at the location x = 0.2 m, as shown. Take a = 0.1m and assume that the loop has a large resistance.
View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.
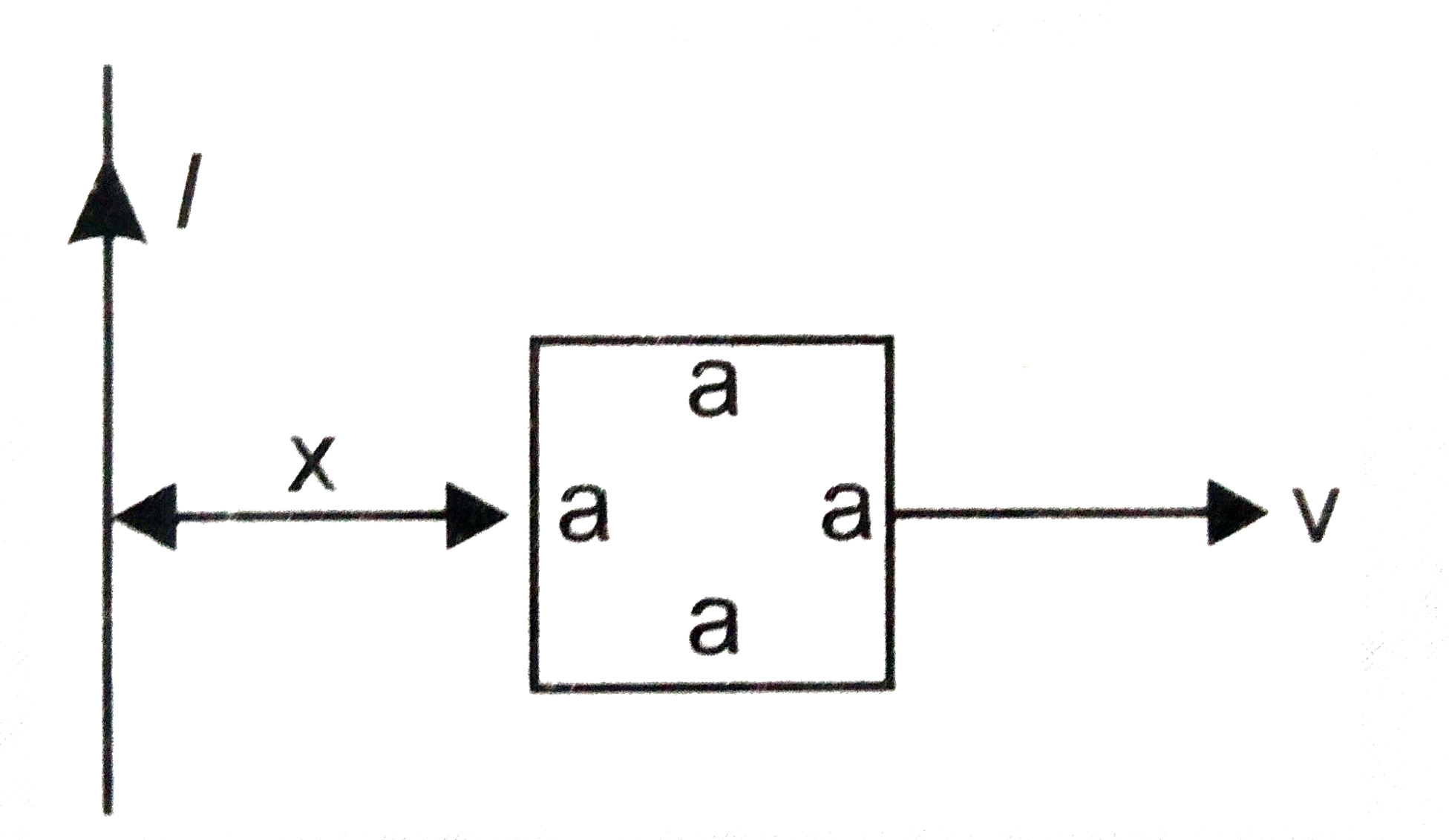
View Solution(a) चित्र 6.21 में दर्शाए अनुसार एक लंबे, सीधे, तार तथा एक वर्गाकार लूप जिसकी एक भुजा की लंबाई a है, के लिए अन्योन्य प्रेरकत्व का व्यंजक प्राप्त कीजिए |
(b) अब मान लीजिए फिर सीधे तार में 50 A की धारा प्रवाहित हो रही है तथा लूप एक स्थिर वेग v=10m/s से दाई ओर को गति कर रहा है | लूप में प्रेरित विद्युत वाहक बल का परिकलन उस क्षण पर कीजिए जब x=0.2 m हो | लूप के लिए a=0.1 m लीजिए तथा यह मान लीजिए कि उसका प्रतिरोध बहुत अधिक है |

View Solution(a) चित्रानुसार एक लंबे, सीधे तार तथा एक वर्गाकार लूप जिसकी एक भुजा की लम्बाई a है के लिए अन्योन्य प्रेरकत्व का व्यंजक प्राप्त कीजिए ।
(b) अब मान लीजिए कि सीधे तार में 50 A की धारा प्रवाहित हो रही है तथा लूप एक स्थितर वेग v=10 मीटर/सेकण्ड से दायीं और गति कर रहा है लूप में प्रेरित वि. वा. बल का परिकलन उस क्षण पर कीजिए जब x=0.2 मीटर हो लूप के लिए a=0.1 मीटर लीजिये तथा यह मान लीजिए कि उसका प्रतिरोध बहुत अधिक है
View SolutionObtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in the figure.

View SolutionNow assume that the straight wire carries a current of 50A and the loop is moved to the right with a constant velocity, upsilon=10m//s . Calculate the induced emf in the loop at the instant when x=0.2m. Take a=0.1m and assume that the loop has a large resistance.
View Solution(b ) अब मान लीजिये की सीधे तार में 50 A की धारा प्रवाहित हो रही है तथा लूप एक स्थिर वेगv=10 m/s से दायी और को गति कर रहा है । लूप में प्रेरित विद्युत वाहक बल का परिकलन उस क्षण पर कीजिए जब x = 0.2 मी हो । लूप के लिए a = 0.1 मी लीजिये तथा यह मान लीजिए की उसका प्रतिरोध बहुत अधिक है ।
View SolutionObtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in fig.
View SolutionNow assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity v=10m.s−1. Calculate the induced emf in the loop at the instant when x = 0.2 m. Take a = 0.1 m and assume that the loop has a large resistance.
View Solutiona. Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in the figure.
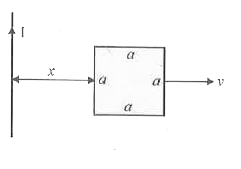
b. Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v=10m/s. Calculate the induced emf in the loop at the instant when x=0.2m. Take a=0.1m and assume that the loop has a large resistance.
View Solution