A square of side L meters lies in the xy-plane in a region, where the magnetic field is given by →B=B0(2ˆi+3ˆj+4ˆk)T where B0 is constant. The magnitude of flux passing through the square isSolution in Gujrati
2B0L2Wb
3B0L2Wb
4B0L2Wb
√29B0L2 Wb
The correct Answer is:C
Area, →A=L2ˆk
→B=B0(2ˆi+3ˆj+4ˆk)
ϕ=→B.→A=B0(2ˆi+3ˆj+4ˆk).L2ˆk
ϕ=4B0L2Wb
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section C Ncert Exemplar Solution (Short Answer )
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section C Ncert Exemplar Solution (Long Answer )
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section B (Numerical) Numerical From DARPAN Based on Textbook
10 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
14 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
Similar Questions
A magnetic field in a certain region is given by →B=B0cos(ωt)ˆk and a coil of radius a with resistance R is placed in the xy-plane with its centre at the origin in the magnetic field (see figure). Find the magnitude and the direction of the current at (a, 0, 0) at t=π2ω,πω and t=3π2ω.
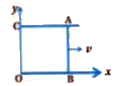
View SolutionA magnetic field →B=B0sin(ωt)ˆk covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d as in figure. The wires are in the xy-plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity ?
View SolutionA conducting circular loop is placed in a uniform magnetic field of 0.04 T with its plane perpendicular to the field. Some how, the radius of the loop starts shrinking at a constant rate of 2 mm/s. Find the induced emf in the loop at an instant when the radius becomes 2 cm solution.
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.

View SolutionA square of side L meters lies in the x-y plane in a region, where the magnetic field is give by B = B_(0) (2 hati + 3 hat j + 4 hatk) T, where B_(0) is constant. The magnitude of flux passing through the square is
View SolutionA square of side x m lies in the x-y plane in a region, when the magntic field is given by vecB=B_(0)(3hati+4hatj+5hatk) T, where B_(0) is constant. The magnitude of flux passing through the square is
View Solutionx-y In an ambient plane where the magnetic field B = B_(0) (2hati + 3hatj + 4hatk) T Is here B_(0) Is a determinant), L is a square of meter arm. The flux magnitude passing through this square is-
View Solutionभुजा x m का एक वर्ग, किसी क्षेत्र में x- y तल में स्थित है, जहाँ चुम्बकीय क्षेत्र →B=B0(3ˆi+4ˆj+5ˆk)T द्वारा दिया गया है, जहाँ B0 नियतांक है। वर्ग में से गुजरने वाले फ्लक्स का परिमाण होगा,
View SolutionL मीटर भुजा का एक वर्ग किसी क्षेत्र में x-y समतल में स्थित है, जहाँ चुम्बकीय क्षेत्र इस प्रकार दिया है,
→B=B0(2ˆi+3ˆj+4ˆk)T,
जहाँ B0, नियतांक है। वर्ग से गुजरने वाले फ्लक्स का परिमाण होगा-
View SolutionL मीटर भुजा वाला एक वर्ग xy-समतल में ऐसे क्षेत्र में रखा है जहाँ चुम्बकीय क्षेत्र B=B0(2ˆi+3ˆk+4ˆk) टेस्ला है, जहाँ B0 नियतांक है। वर्ग से गुजरने वाला चुम्बकीय फ्लक्स का परिमाण है
View SolutionA square of side LM lies in the xy plane in a region, when the magnetic field is given by →B=B0(2ˆi+3ˆj+4ˆk) T where B0is constant. The magnitude of flux passing through the square is …..Wb.
View SolutionA square of side L meters lies in the x-y plane in a region, where the magnetic field is given by B=B0(2ˆi+3ˆj+4ˆk)T, where B0 is constant. The magnitude of flux passing through the square is
View SolutionA square of side L meters lies in the x-y plane in a region where the magnetic field is given by →B=B0(2ˆi+3ˆj+4ˆk)T Where B0 is constant. The magnitude of flux passing through the square is
View SolutionA square of side x m lies in the x-y plane in a region, when the magntic field is given by →B=B0(3ˆi+4ˆj+5ˆk) T, where B0 is constant. The magnitude of flux passing through the square is
View Solution
