A loop, made of straight edges has six corners at A(0,0,0), B(L,0,0) ,C(L,L,0), D(0,L,0), E(0,L,L) and F(0,0,L). A magnetic field is present in the region. The flux passing through the loop ABCDEFA (in that order) isSolution in Gujrati
The correct Answer is:B
Consider a plane is made by two loop.
Area of loop ABCDA in xy-plane ,
Area of loop ADEFA in yz- plane
Total area of loops are
Now flux linked with these loops is
where
Magnetic flux ,
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section C Ncert Exemplar Solution (Short Answer )
Explore 5 Videos
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section C Ncert Exemplar Solution (Long Answer )
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section B (Numerical) Numerical From DARPAN Based on Textbook
Explore 10 Videos
- ELECTRIC CHARGES AND FIELDS Book:KUMAR PRAKASHANChapter:ELECTRIC CHARGES AND FIELDS Exercise:SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
Explore 14 Videos
- ELECTROMAGNETIC WAVESBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC WAVESExercise:BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
Explore 5 Videos
Similar Questions
A magnetic field in a certain region is given by →B=B0cos(ωt)ˆk and a coil of radius a with resistance R is placed in the xy-plane with its centre at the origin in the magnetic field (see figure). Find the magnitude and the direction of the current at (a, 0, 0) at t=π2ω,πω and t=3π2ω.
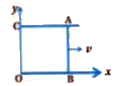
View SolutionA magnetic field →B=B0sin(ωt)ˆk covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d as in figure. The wires are in the xy-plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity ?
View SolutionA conducting circular loop is placed in a uniform magnetic field of 0.04 T with its plane perpendicular to the field. Some how, the radius of the loop starts shrinking at a constant rate of 2 mm/s. Find the induced emf in the loop at an instant when the radius becomes 2 cm solution.
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.

View SolutionA loop made of straight edegs has six corners at A(0,0,0), B(L, O,0) C(L,L,0), D(0,L,0) E(0,L,L) and F(0,0,L) . Where L is in meter. A magnetic field B = B_(0)(hat(i) + hat(k))T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View Solutionमूल्यांकन कीजिए -
∣∣ ∣ ∣ ∣∣almn0bpq00cr000d∣∣ ∣ ∣ ∣∣
View SolutionA loop, made of straight edges has six corners at A(0,0,0), B(L,0,0), C(L,L,0), D(0,L,0), E(0,L,L) and F(0,0,L). A magnetic field →B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is:
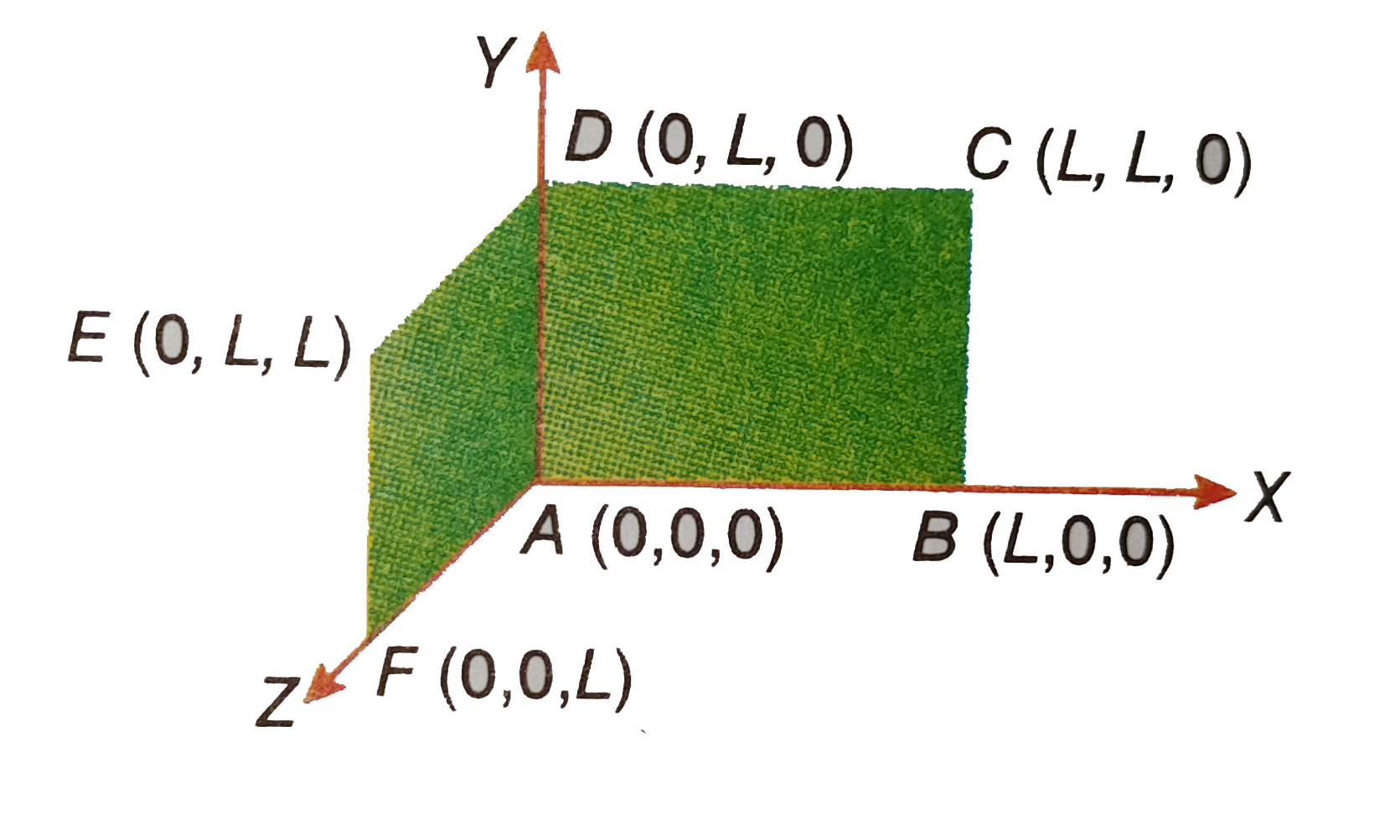
View SolutionIf A=⎡⎢ ⎢ ⎢⎣k2000l2000m4⎤⎥ ⎥ ⎥⎦andA−1=⎡⎢ ⎢ ⎢⎣120001300014⎤⎥ ⎥ ⎥⎦ then k+l+m=
View SolutionA loop ABCA of straight edges has three corner points A (8, 0, 0), B (0, 8, 0 ) and C (0, 0, 8). The magnetic field in this region is →B=5(ˆi+ˆj+ˆk)T0 . The quantity of flux through the loop ABCA (in Wb) is _____.
View Solutionसीधी कोरों से बने एक लूप में A(0, 0, 0), B(L, 0, 0), C(L, L, 0), D(0, L, 0), E(0, L, L), F(0, 0, L) पर छह कोने हैं। एक चुम्बकीय क्षेत्र →B=B0(ˆi+ˆk)T क्षेत्र में उपस्थित है। लूप ABCDEFA (उसी क्रम में) से गुजरने वाला फ्लक्स होगा-
View Solutionएक लूप सीधी भुजाओं से बना है, जिसमें छः कोने A(0,0,0),B(L,0,0),C(L,L,0),DO,L,0),E(0,L,L) तथा F(0.0,L) पर हैं। इस क्षेत्र में एक चुम्बकीय क्षेत्र B=B0(ˆi+ˆk) टेस्ला विद्यमान है। लूप ABCDEFA से गुजरने वाला फ्लक्स है
View SolutionA loop made of straight edges has six corners at A(0,0,0), B(L, O,0), C(L,L,0), D(0,L,0), E(0,L,L) and F(0,0,L) . Where L is in meter. A magnetic field B = B_(0)(hat(i) + hat(k))T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionIf A=⎡⎢ ⎢ ⎢⎣k2000l2000m4⎤⎥ ⎥ ⎥⎦andA−1=⎡⎢ ⎢ ⎢⎣120001300014⎤⎥ ⎥ ⎥⎦ then k+l+m=
View Solution