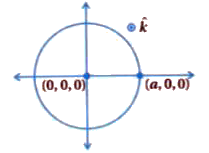
A magnetic field in a certain region is given by →B=B0cos(ωt)ˆk and a coil of radius a with resistance R is placed in the xy-plane with its centre at the origin in the magnetic field (see figure). Find the magnitude and the direction of the current at (a, 0, 0) at t=π2ω,πω and t=3π2ω. Solution in Gujrati
Magnetic flux linked with coil,
ϕ=→B.→A=BAcosθ=BA
ϕ=B0(πa2)cosωt[∵A=πa2]
Induced emf,
ε=dϕdt=−ddt(B0πa2cosωt)
=−B0πa2[−ωsinωt]
ε=B0πa2ωsinωt
Induced current I=εR=B0πa2ωRsinωt
At t=π2ωtime,
I=B0πa2ωRsin(ω×π2ω)
I=B0πa2ωR
Now according to →B=B0cos(ωt)ˆk magnetic flux came out from coil decreases (cos is decreasing function for t = 0 to t=πω ). Hence, according to Lenz.s law induced current will try to increase that outward flux. For that induced current will flow in anticlockwise direction so at (a, 0, 0) current is along +ˆj direction.
At t=πω time
I=B0πa2ωRsin(ω×πω)=0
At t=3π2ω time
I=B0πa2ωRsin(ω×3π2ω)
=B0πa2ωRsin(3π2)
I=−B0πa2ωR
Negative sign appearing here indicates that induced current at (a, 0, 0) is in −ˆj direction. [According to case (i)]
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section C Ncert Exemplar Solution (Long Answer )
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section D MCQs (From DARPAN Based on Textbook )
Explore 121 Videos
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section C Ncert Exemplar Solution (MCQs)
Explore 16 Videos
- ELECTRIC CHARGES AND FIELDS Book:KUMAR PRAKASHANChapter:ELECTRIC CHARGES AND FIELDS Exercise:SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
Explore 14 Videos
- ELECTROMAGNETIC WAVESBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC WAVESExercise:BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
Explore 5 Videos
Similar Questions
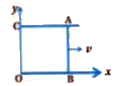
A magnetic field →B=B0sin(ωt)ˆk covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d as in figure. The wires are in the xy-plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity ?
View SolutionWhen a metallic rod falls freely, keeping its length horizontal and parallel to north-south direction, emf induced across it is ______
View SolutionA square of side L meters lies in the xy-plane in a region, where the magnetic field is given by →B=B0(2ˆi+3ˆj+4ˆk)T where B0 is constant. The magnitude of flux passing through the square is
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.

View SolutionShows a coil placed in a decreasing magnetic field applied perpendicular to the plane of the coil. The magnetic field is decreasing at a rate of 10Ts−1. Find out current in magnitude and direction of current.

View SolutionA magnetic field in a certain region is given by B=B0cos(ωt)ˆk and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field, Fig. Find the magnitude and the direction of the current at (a,0,0) att=π/2ω,t=π/ω and t=3π/2ω.

View SolutionFind the rms value of current i=I_(m)sin omegat from (i) t=0 "to" t=(pi)/(omega) (ii) t=(pi)/(2omega) "to" t=(3pi)/(2omega)
View SolutionIn a region of space, magnetic field exists in a cylindrical region of radius a centred at origin with magnetic field along negative z-direction. The field is given by vecB=-B_(0)thatk . The force experienced by a stationary charge q placed at (r, 0, 0), where r gt a is
View SolutionA circular conducting coil of radius a and resistance R is placed with its plane perpendicular to a magnetic field. The magnetic field varies with time according to the equation B=B_(0)sinomegat . Obtain the expression for the induced current in the coil.
View SolutionA circular coil of rauis 10cm, 500 turns and resistance 2Ω is placed with its plane perpendicualr to the horizontal component of the earth's magnetic field it is rotated about its vertical diameter through 180∘ in 0.25 S estimate the magnitude of the emf and current induced in the coil. Horizontal component of earth's magnetic field at the place is 3×10−5T.
View SolutionThe electric field component of a monochromatic radiation is given by
→E=2E0ˆicoskzcosωt
Its magnetic field →B is then given by :
View SolutionA square of side L meters lies in the xy-plane in a region, where the magnetic field is given by →B=B0(2ˆi+3ˆj+4ˆk)T where B0 is constant. The magnitude of flux passing through the square is
View SolutionA circular loop of radius R is placed in the uniform magnetic field. The value of magnetic field changes is given by equation B=B_0 e^(-t/tau) . Where B_0 and tau are constants. The emf induced in the coil is ____
View SolutionA magnetic field in a certain region is given by B = B_(0) cos (omega t) hat k and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field, Fig. Find the magnitude and the direction of the current at (a,0,0) at t = pi//2 omega, t = pi//omega and t = 3 pi//2 omega .
View Solution