A circular loop of radius R is placed in the uniform magnetic field. The value of magnetic field changes is given by equation B=B0e−tτ . Where B0 and τ are constants. The emf induced in the coil is ____ Solution in Gujrati
π2B0e−tτ×10−2 V
πR2B0τe−tτ
π2B0τe−tτ
None of these
The correct Answer is:B
ϕ=AB=πr2B0e−tτ
∴ε=−dϕdt
=−ddt[πr2B0e−tτ]
∴ε=−πR2B0ddt(e−tτ)
=−πR2B0(−1τ.e−tτ)
∴ε=πR2B0τe−tτ
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )
38 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section C Ncert Exemplar Solution (Long Answer )
11 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
14 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
Similar Questions
Three pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......

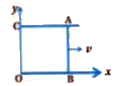
View SolutionA magnetic field →B=B0sin(ωt)ˆk covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d as in figure. The wires are in the xy-plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity ?
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.

View SolutionA conducting loop of area 5.0cm2 is placed in a magnetic field which varies sinusodially with time as B=B0sinωt where B0=0.20T and ω=300s−1. The normal to the coil makes an angle of 60∘ with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ=(τ900)s and (c) the emf induced at t=(π600)s.
View SolutionA loop of wire enclosing an area S is placed in a region where the magnetic field is perpendicular to the plane. The magnetic field B varies with time according to the expression B=B_0e^(-at) where a is some constant. That is, at t= 0 . The field is B_0 and for t gt 0 , the field decreases exponentially. Find the induced emf in the loop as a function of time.
View SolutionThe (τ−θ) graph for a current carrying coil placed in a uniform magnetic field is
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B = B_0e^(-t//tau) , where B_0 and tau are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t to oo) is :
View SolutionA circular wire loop of radius r lies in a uniform magnetic field B, with its plane perpendicular to magnetic field. If the loop is deformed to a square shape in the same plane in time t, the emf induced in the loop is
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View SolutionA coil having an area A_0 is placed in a magnetic field which changes from B_0 to 4B_0 in time interval t. The emf induced in the coil will be
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View SolutionA uniform magnetic field is restricted within a region of radius 1m. The magnetic field changes with time(t) as →B=B0(2t3)ˆk. A loop of radius 2m is outside the region of magnetic field as shown in figure. The emf induced in loop is
_PHY_E06_055_Q01.png)
View Solutionएक धारावाही वृत्ताकार कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र B0 हो, तो उसकी त्रिज्या आधी कर देने पर वहाँ चुम्बकीय क्षेत्र हो जाएगा, यदि धारा वही रहे
View SolutionA loop of wire enclosing an area S is placed in a region where the magnetic field is perpendicular to the plane. The magnetic field B varies with time according to the expression B=B_0e^(-at) where a is some constant. That is, at t= 0 . The field is B_0 and for t gt 0 , the field decreases exponentially. Find the induced emf in the loop as a function of time.
View Solution
