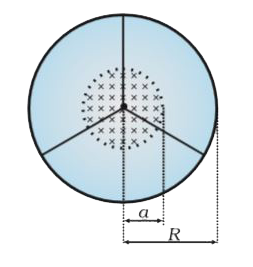
A line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig.) . A uniform magnetic field extends over a circular region within the rim. It is given by,
B=−B0K(r≤a,a<R)=0(otherwise)
 Solution in Telugu
Solution in Telugu
−Bπa2λMRˆk
Similar Questions
A line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light nonconducting spokes and is free to rotate without friction about its axis as per figure. A uniform magnetic field extends over a circular region within the rim. It is given by,
B=−B0k(r≤a,a<R)
=0 (otherwise)
What is the angular velocity of the wheel after the field is suddenly switched off ?
View SolutionA line charge lambda per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig. 6.22). A uniform magnetic field extends over a circular region within the rim. It is given by, B=B_(0)k" "(ra le a,a lt R) =0 " " (otherwise) What is the angular velocity of the wheel after the field is suddenly switched off?
View SolutionA line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light nonconducting spokes and is free to rotate without friction about its axis as per figure. A uniform magnetic field extends over a circular region within the rim. It is given by,
B=−B0k(r≤a,a<R)
=0 (otherwise)
What is the angular velocity of the wheel after the field is suddenly switched off ?
View SolutionA wheel having n conducting concentric spokes is rotating about it geometrical axis with an angular velocity omega , in a uniform magnetic field B perpendicular to its plane prove that the induced emf generated between the rim of the wheel and the center is (omegaBR^2)/2 , where R is the radius of the wheel. It is given that the rim of the wheel is conducting.
View SolutionA line charge lambda per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig. 6.08). A uniform magnetic field extends over a circular region within the rim. It is given by, vecB = - B_(0)hatk (r le a, aItR) = 0 (otherwise) What is the angular velocity of the wheel after the field is suddenly switched off ?
View SolutionA wheel with 4 spokes is placed with its plane perpendicular to a uniform magnetic field B of magnitude 0.5 T. The field is directed into the plane of the paper and is present over the entire region of the wheel as shown in Fig. When the switch S is closed, there is initial current of 6 A between the axis and the rim and the wheel begins to rotate. Resistances of the spokes are 1, 2, 4 and 8 Ω, respectively. Resistance of rim is negligible.
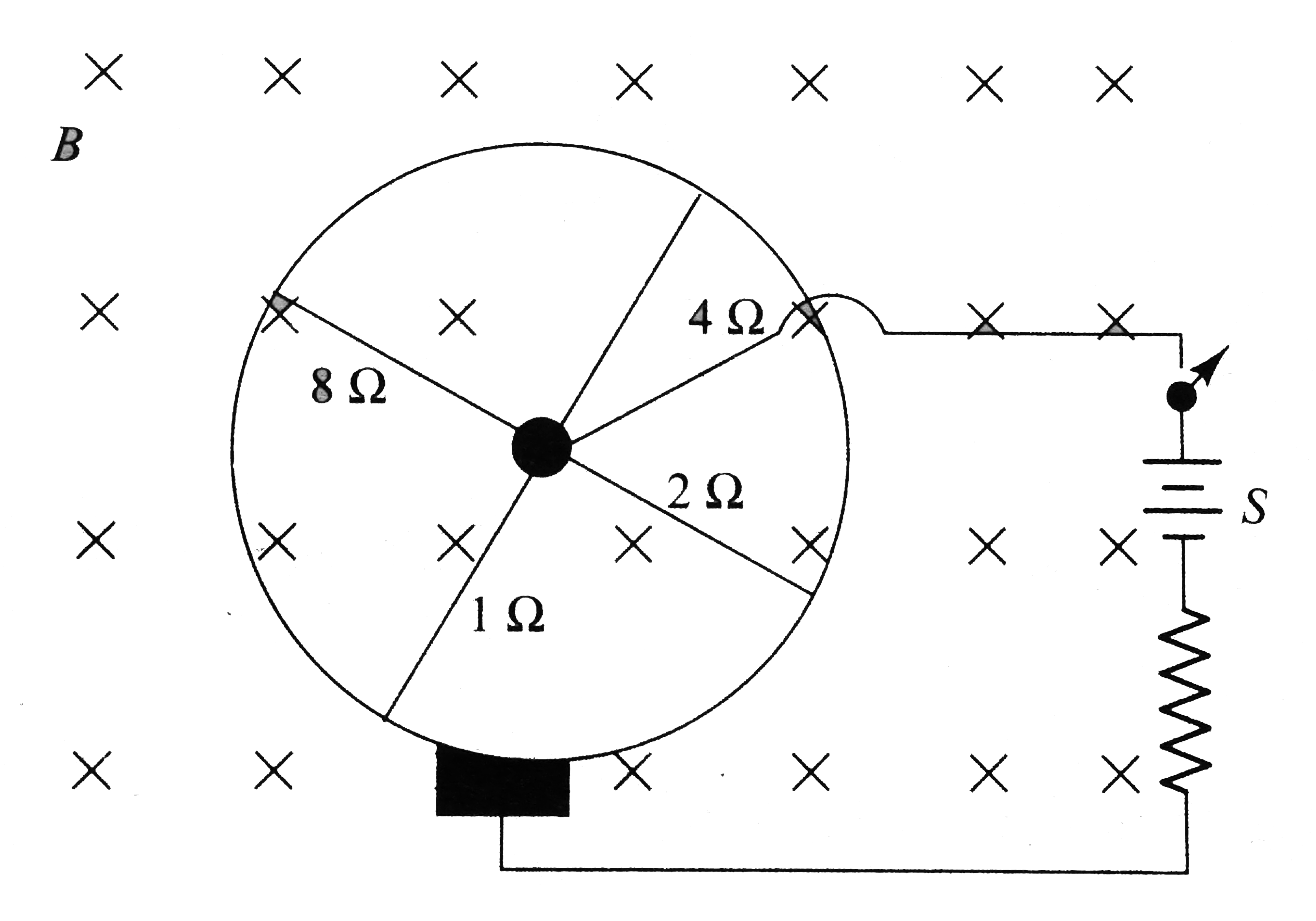
a. What is the direction of rotation of the wheel?
b. Radius of the wheel is 0.2 m. Calculate initial torque acting on the wheel.
View SolutionA metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity omega in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)
View Solution
