A line charge lambda per unit length is lodged uniformly onto the rim

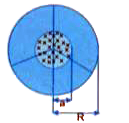
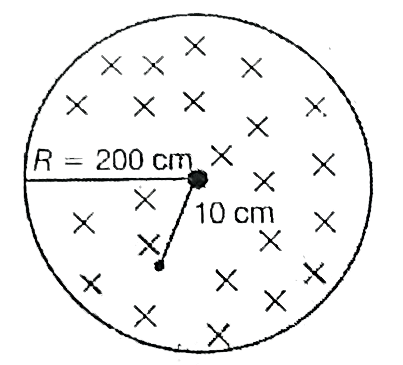
A line charge $λ$ per unit length is pasted uniformly on to the wire of a wheel of mass $m$ and radius $R$ . The wheel has light non-conducting spokes and is free to rotate about a vertical axis as shown in $F i g . 3.166$ . A uniform magnetic field extends over a radial rigion of radius $r$ given by $B = - B_{0} ˆ k (r \leq a, a < R) = 0$ (otherwise). What is the angular velocity of the wheel this field is suddenly switched off?

A(a) $\frac{- 2 B_{0} π a^{2} r}{m R} ˆ k$
B(b) $\frac{- 2 B_{0} π a^{2} r}{3 m R} ˆ k$
C( c) $\frac{B_{0} π a^{2} λ}{m R} ˆ k$
D( d) $\frac{- B_{0} π a^{2} λ}{m R} ˆ k$
The moment of inertia of a disc of mass $M$ and radius $R$ about a tangent to its rim in its plane is
A $\frac{2}{3} M R^{2}$
B $\frac{3}{2} M R^{2}$
C $\frac{4}{5} M R^{2}$
D $\frac{5}{4} M R^{2}$
A wheel comprises a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is

A $(M + \frac{m}{4}) R^{2}$
B $(M + m) R^{2}$
C $(M + 3 m) R^{2}$
D $(\frac{M + m}{2}) R^{2}$

The moment of inertia of a disc of mass $M$ and radius $R$ about a tangent to its rim in its plane is