A family of lines is given by (1+2λ)x+(1−λ)y+λ=0 being a parameter . The line belonging to this family at the maximum distance from the point (1,4) is ax+by+c=0 , then find the value of a+b+c16
4x - y + 1 = 0
33x + 12y 7 = 0
12 x + 33y = 7
none of these
The correct Answer is:C
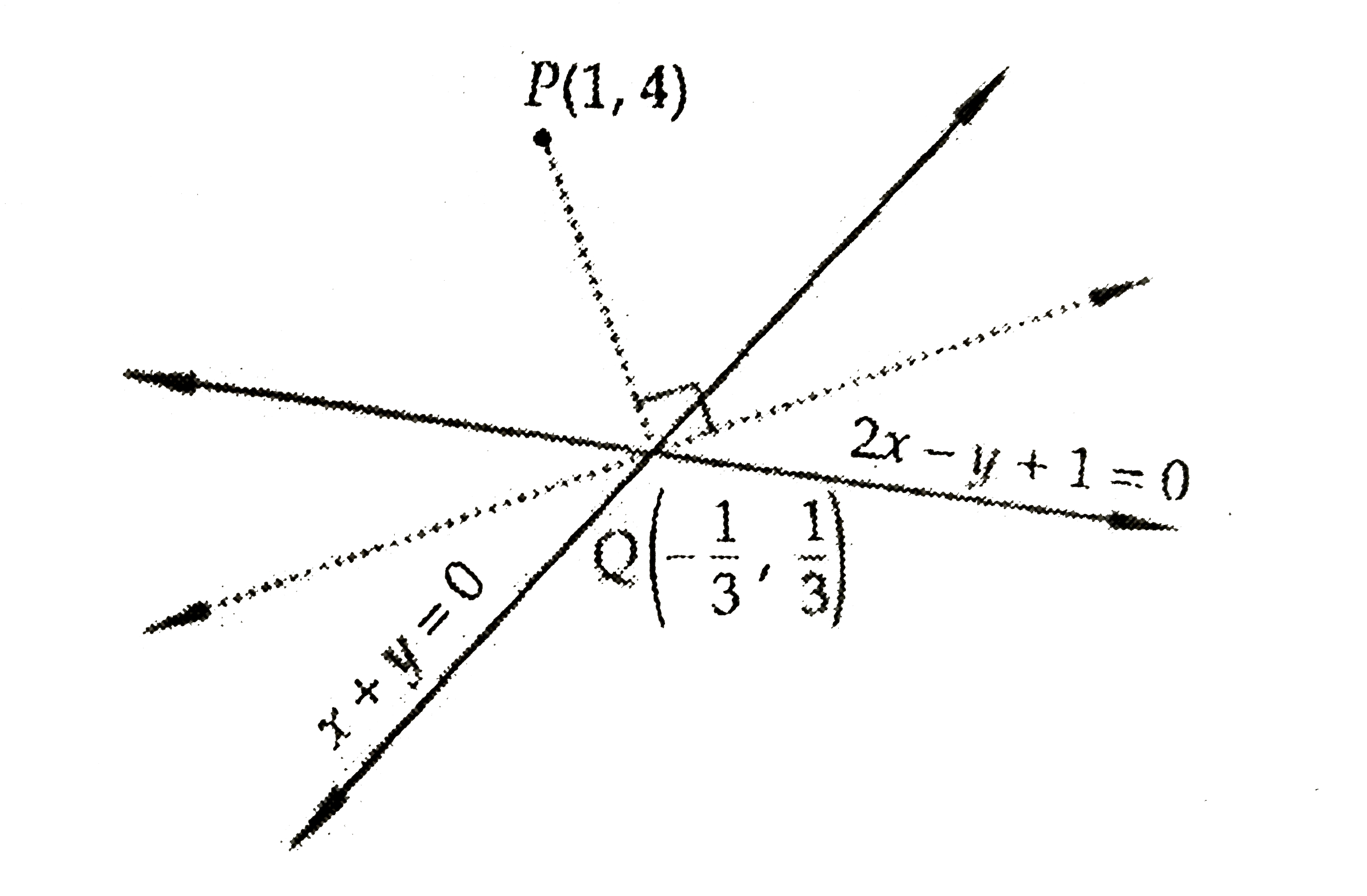
We have , x + y + λ(2x−y+1)=0
Clearly , it represents a family of lines passing through the intersection of the lines x + y = 0 and 2x - y + 1 = 0 i.e., the point (-1/3 , 1/3).
The required the line passes through (-1/3 , 1/3) and is perpendicular to the line joining (1,4) and (-1/3 , 1/3) . So , its equation is
y−13=−411(x+13)⇒12x+33y=7
Topper's Solved these Questions
- STRAIGHT LINESBook:OBJECTIVE RD SHARMAChapter:STRAIGHT LINESExercise:Section-1 Solved MCQs (Example)
Explore 1 Video
- STRAIGHT LINESBook:OBJECTIVE RD SHARMAChapter:STRAIGHT LINESExercise:SECTION - II (ASSERTION - REASON TYPE MCQs)
Explore 14 Videos
- STRAIGHT LINESBook:OBJECTIVE RD SHARMAChapter:STRAIGHT LINESExercise:ILLUSTRATION 18
Explore 1 Video
- SETSBook:OBJECTIVE RD SHARMAChapter:SETSExercise:Chapter Test
Explore 30 Videos
Similar Questions
A family of lines is given by (1+3λ)x+2λy−1(1−3λ)=0. If one of the bisectors of two of the members of the family has equation x+y+2=0. Find the equation of other bisector
View SolutionGiven a family of lines a(2x +y+4) + b(x-2y-3)=0 .The number of lines belonging to the family at a distance of √10 from point (2,−3) is
View Solution
Knowledge Check
The equation (1+2k)x+(1−k)y+k=0,k being parameter represents a family of lines. The line which belongs to this family and is at a maximum distance from the point (1,4) is
A33x+12y+7=0B12x+33y−7=0C4x−y+7=0D12x−33y+7=0Given the family of lines
a(2x+y+4)+b(x−2y−3)=0. The number of lines belonging to the family at a distance √10 from any point (2,-3) isA0B1C2D4A family of curve S is given by S≡x2+2xy+y2−4x(1−λ)−4y(1+λ)+4, then S=0 represents
Apair of straight line ∀λ∈RBstraight line for exactly one value of λCparabola ∀λ∈R−{0}Dellipse for three values of λ
Prove that the family of lines represented by x(1+λ)+y(2−λ)+5=0,λ being arbitrary, pass through a fixed point. Also find the fixed point.
View SolutionConsider a family of straight lines (x+y)+λ(2x−y+1)=0 . Find the equation of the straight line belonging to this family that is farthest from (1,−3).
View SolutionConsider a family of straight lines (x+y)+λ(2x−y+1)=0 . Find the equation of straight line belonging to this family that is farthest from (1;-3)
View SolutionIf L1andL2, are two lines belonging to family of lines (3+2λ)x+(4+3λ)y−7−5λ=0 (λ is parameter) such that it is at maximum and miimum distance from (2, 3), respectively, then theequation of lines passing through (1,2) and making equal angles with L1andL2 is/are
View SolutionConsider a set of all the lines (2+λ)x−(3+2λ)y+(1+λ)=0,λ∈R, then equation of the line which belongs to this set & farthest from origin is :
View Solution
