Let A and B have coordinates (x1,y1) and (x2,y2) respectively . We define the distance between A and B as
d (A , B) = max {|x2−x1|,|y2−y1|}
If d ( A, O) = 1 , where O is the origin , then the locus of A has an area of

A

1sq. Unit

B

2 sq. units

C

4sq. units

D

1/4 sq. units

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Let the coordinates of A be (h ,k) . Then ,
d(A,O) = 1
⇒ max {|h| , |k|} = 1
⇒|h|≤1
⇒ Locus of A (h,k) is |x|≤1,|y|≤1
Clearly , |x|≤1 and |y|≤1 represent the region enclosed by the square shown in fig. 40 .
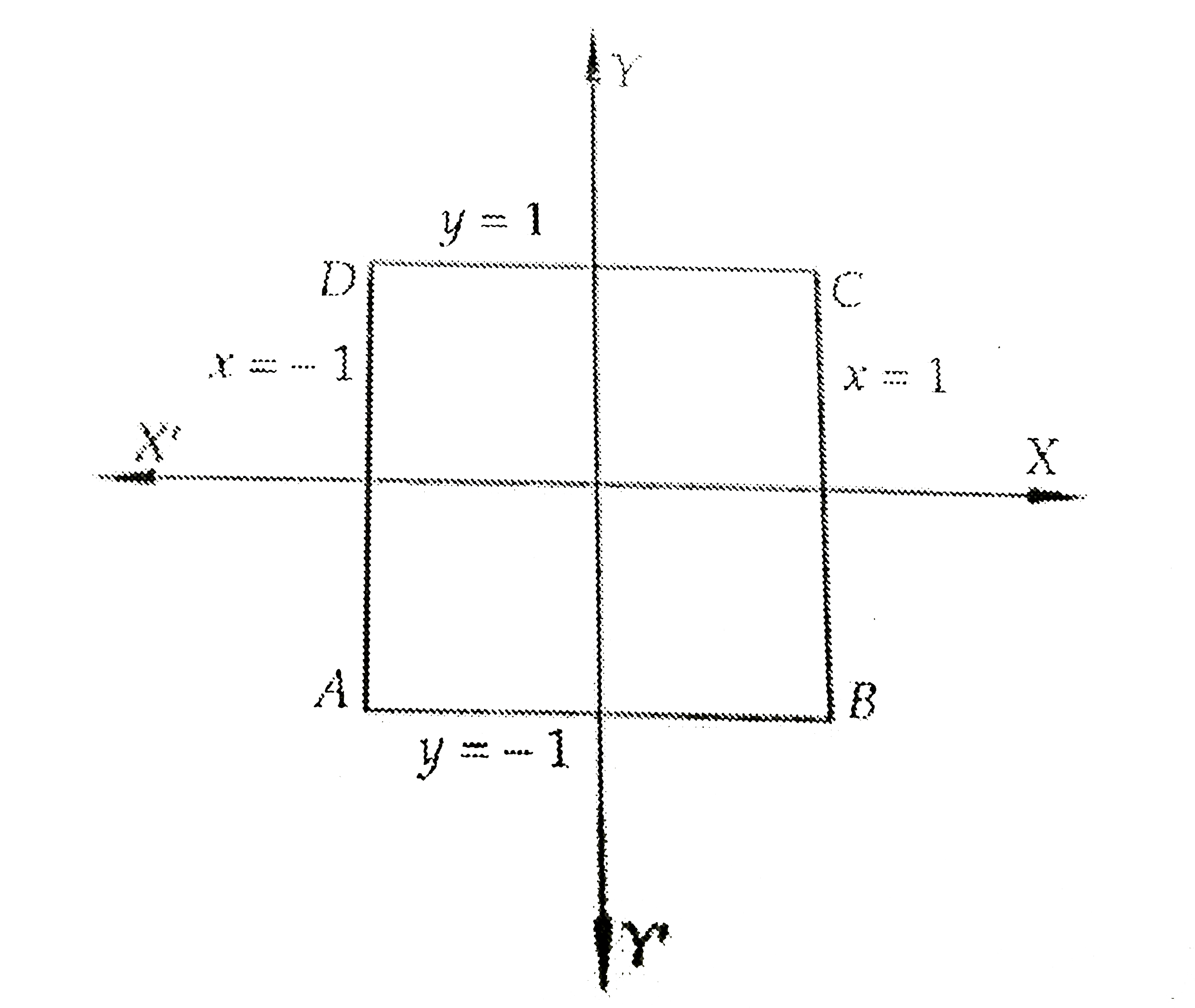
ocr_image
∴ Area enclosed by the locus of A = 2×2=4sq. units

Updated on:21/07/2023
|
Class 11MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Consider a three dimensional Cartesian system with origin at O and three rectangular coordinate axes x,y and z-axis. Suppose that the distance between two points P and Q in the space having their coordinates (x1,y1,z1)and(x2,y2,z2) respectively be defined by the following formula d(P,Q)=|x2−x1|+|y2−y1|+|z2−z1|
    Although the rormula of distance between two points has been defined in a new way, yet the other definition remain same (like section formula, direction consines ets). So, in general equations of straight line in space, plane in spece remain unchanged.
    Let A be a point (5,2,3) in the given reference system. Then locus of the point P in the fiest octant satisfying the equation d(O,P)=d(A,P) does not contain

    Aany of the coordinates axes
    Bany of the coordinates planes
    Cany plane parallel to coordinates axes planes
    Dany plane parallel to coordinates

  • Consider a three dimensional Cartesian system with origin at O and three rectangular coordinate axes x,y and z-axis. Suppose that the distance between two points P and Q in the space having their coordinates (x1,y1,z1)and(x2,y2,z2) respectively be defined by the following formula d(P,Q)=|x2−x1|+|y2−y1|+|z2−z1|
    Although the rormula of distance between two points has been defined in a new way, yet the other definition remain same (like section formula, direction consines ets). So, in general equations of straight line in space, plane in spece remain unchanged.
    Locus of point P if d (O,P) = k, where ,k is a positive constnat number, represents

    Aa sphere of radius k
    Ba set of eight planes forming an octhedron
    Ca set of eight planes forming hexagonal prism
    Dan infinite cylinder of radius k

  • If A (x1,y1) and B(x2,y2) are point on y2=4ax , then slope of AB is

    Ax1−x2y1−y2
    B4ax1+x2
    C4ay1+y2
    D4ax1−x2