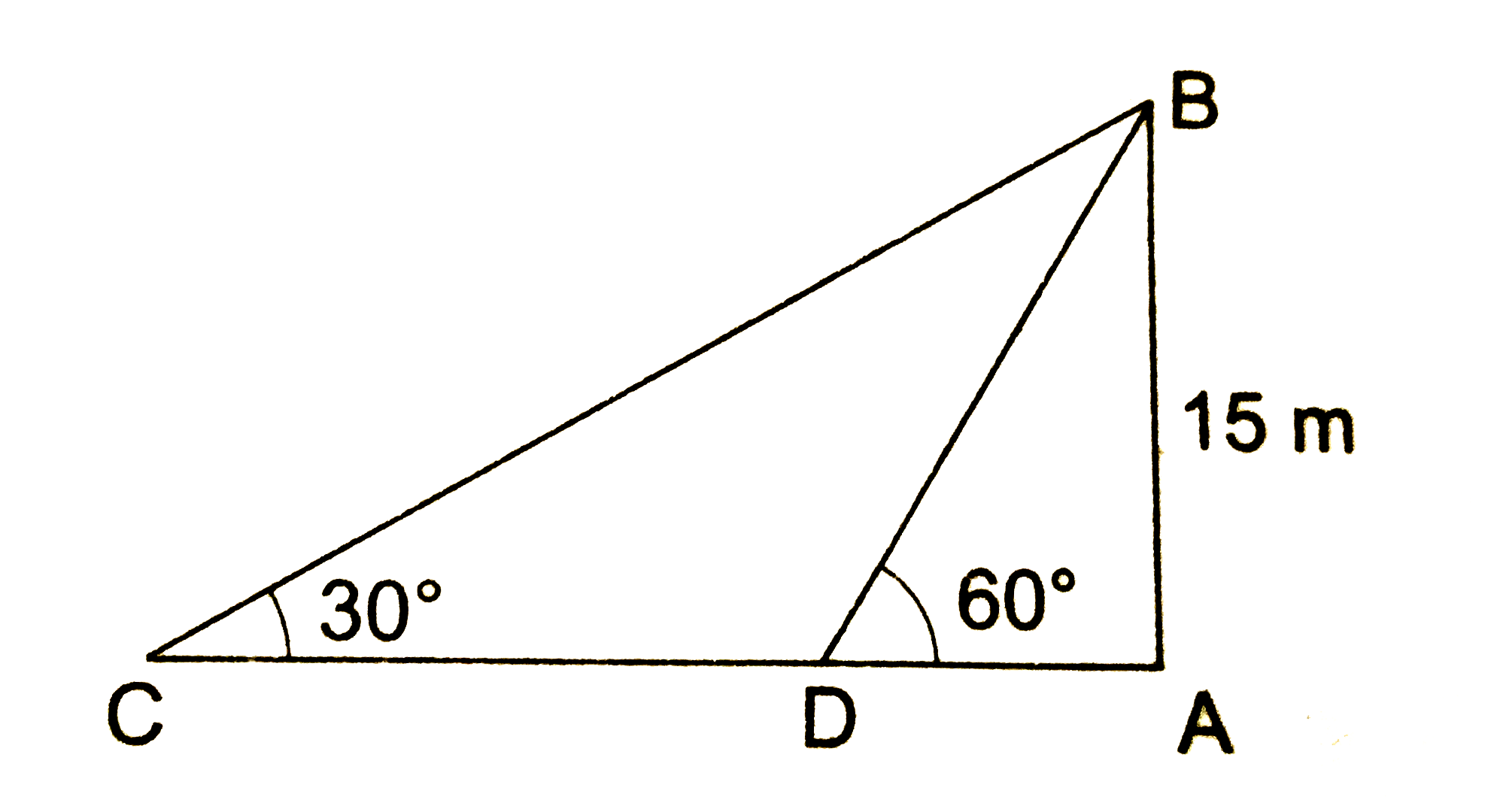
If the elevation of the sun changes from 30∘ to 60∘ then the difference between the lengths of shadow of a pole 15 m high, is

A

7.5m

B

15m

C

10√3m

D

5√3m

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Let AB be the pole and AC and AD be its shadows when ∠ACB=30∘ and ∠ADB=60∘
From right ΔCAB, we have
ACAB=cot30∘⇒AC15m=√3
⇒AC=15√3m……….(i)
From right ΔDAB, we have
ADAB=cot60∘⇒AD15m=1√3⇒AD=15m√3
⇒AD=15m√3×√3√3=5√3m..........(ii)
Required difference =(15√3−5√3)m=10√3m.
ocr_image

Updated on:21/07/2023
|
Class 10MATHSSOME APPLICATIONS OF TRIGONOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If the elevation of the Sun changes from 30∘ to 60∘ , then the difference between the lengths of shadows of a pole 15 metre high is

    A7. 5 metre
    B15 metre
    C10√3 metre
    D5√3 metre

  • If the angle of elevation of the sun changed from 45∘ to 60∘ , then the length of the shadow of a pillar decreases by 10 m .The height of the pillar is :

    A5(3−√3) metre
    B5(√3+1) metre
    C15(√3+1) metre
    D5(3+√3) metre

  • If the angle of elevation of the sun decreases from 45∘ to30∘ , then the length of the shadow of a pillar increases by 60m . The height of the pillar is

    A60(√3+1)metre
    B30(√3−1)metre
    C30(√3+1) metre
    D30(√3−1) metre