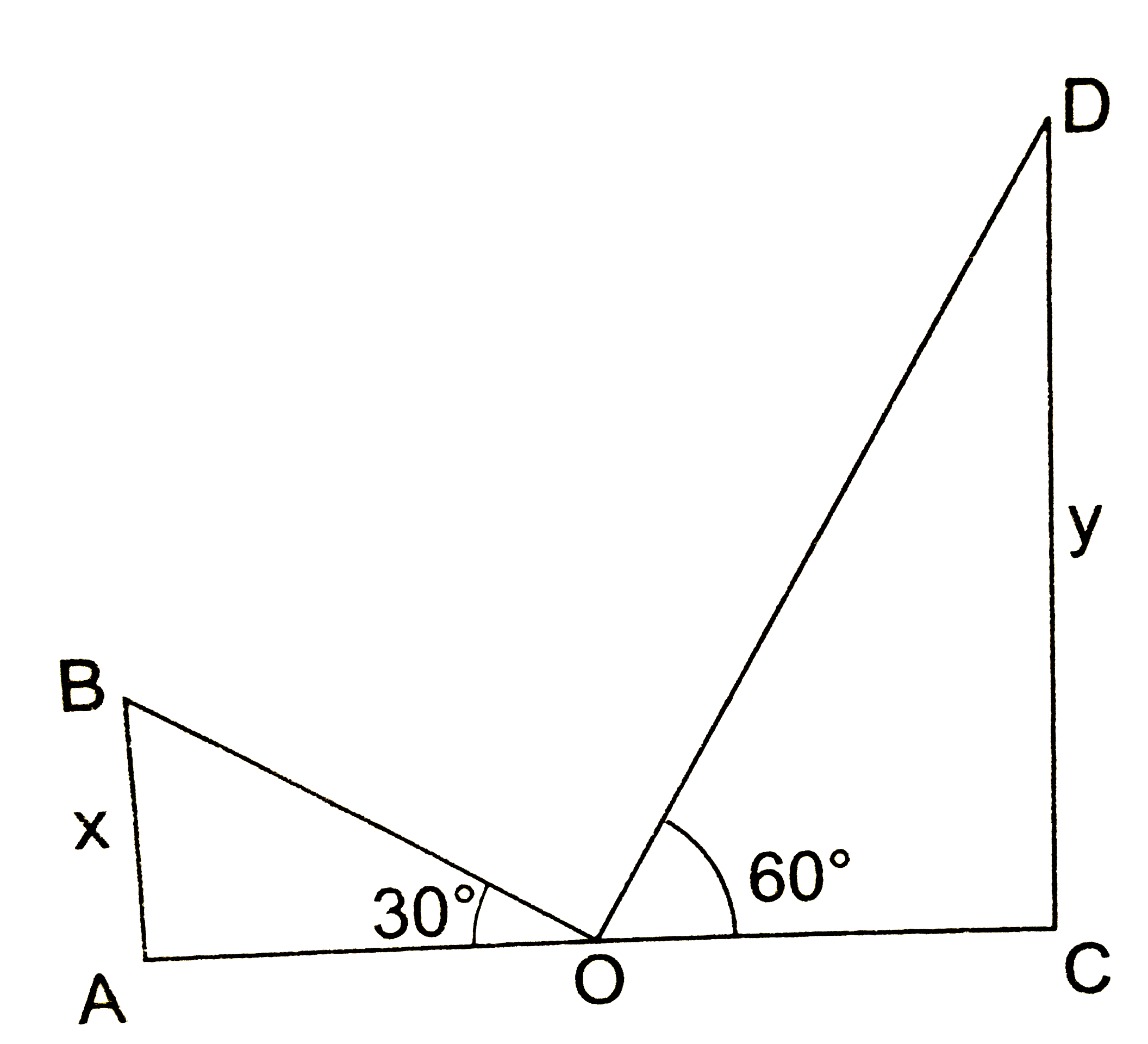
The tops of two towers of height x and y , standing on level ground, subtend angles of 30∘ and 60∘ respectively at the centre of the line joining their feet, then find x :y .
1:1
2:1
1:3
3:1
The correct Answer is:C
Let AB and CD be the given pillars and O be the midpoint of AC. Then, AB=x,CD=y,∠AOB=30∘ and ∠COD=60∘.
From right ΔOAB, we have
OAAB=cot30∘⇒OAx=√3.
⇒OA=x√3……….(i)
From right ΔOCD , we have
OCOD=cot60∘⇒OCy=1√3⇒OC=y√3.........(ii)
But, OA=BC
∴x√3=y√3⇒3x=y⇒xy=13⇒x:y=1:3.
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBook:RS AGGARWALChapter:HEIGHTS AND DISTANCESExercise:Exercise 14
Explore 38 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Multiple Choice Questions (Mcq)
Explore 34 Videos
- LINEAR EQUATIONS IN TWO VARIABLES Book:RS AGGARWALChapter:LINEAR EQUATIONS IN TWO VARIABLES Exercise:QUESTION
Explore 2 Videos
Similar Questions
The tops of two towers of height x and y , standing on level ground, subtend angles of 30o and 60o respectively at the centre of the line joining their feet, then find x :y .
View SolutionIf two towers of height h1 and h2 subted angle of 60∘ and 30∘ respectively at the mid point of the line joining their feet, then find h1:h2.
View Solution
Knowledge Check
A tower of height h stands at a point O on the ground. Two poles of height a and b stand at the points A and B respectively such that O lies on the line joining A and B. If the angle of elevation of the top of the tower at the foot of one pole is ame as at the top of the other pole, then h is equal to
Aa+babBaba+bCa + bDa+b|a−b|The angles of elevation of the top of a tower at the top and the foot of a pole 10 m high are 30∘and60∘ respectively. The height of the tower is
A15 mB20 mC10√3 mD25√3 mThe angles of elevation of the top of a tower standing on a horizontal plane, from two points on a line passing through its foot at distances a and b, respectively, are complementary angles. If the line joining the two points subtends an angle θ at the top of the tower, then if a>b,sinθ =
Aa−ba+bBa+ba−bC2√aba+bD2√aba−b
The angles of elevation of the top of a tower at the top and the foot of a pole of height 10 m are 30∘and60∘ respectively. The height of the tower is
(A). 10m
(B). 15m
(C). 20m
(D). None of these
View SolutionA vertical tower PQ subtends the same anlgle of 30∘ at each of two points A and B ,60 m apart on the ground .If AB subtends an angle of 120∘ at p the foot of the tower ,then find the height of the tower .
View SolutionThe angles of elevation of the top of a tower standing on a horizontal plane from two points on a line passing through the foot of the tower at distances a and b respectively are complementry angles. If the line joning the two points subtend an angle θ at the top of the tower then h=____and sinθ=____.
View SolutionThe angle of elevation of the top of a tower from the top and bottom of a building of height 'a' are 30∘ and 45∘ respectively. If the tower and the building stand at the same level , the height of the tower is
View SolutionFrom the top of a building, the angle of elevation and depression of top and bottom of a tower are 60∘and30∘ respectively. If the height of the building is 5 m, then find the height of the tower.
View Solution

