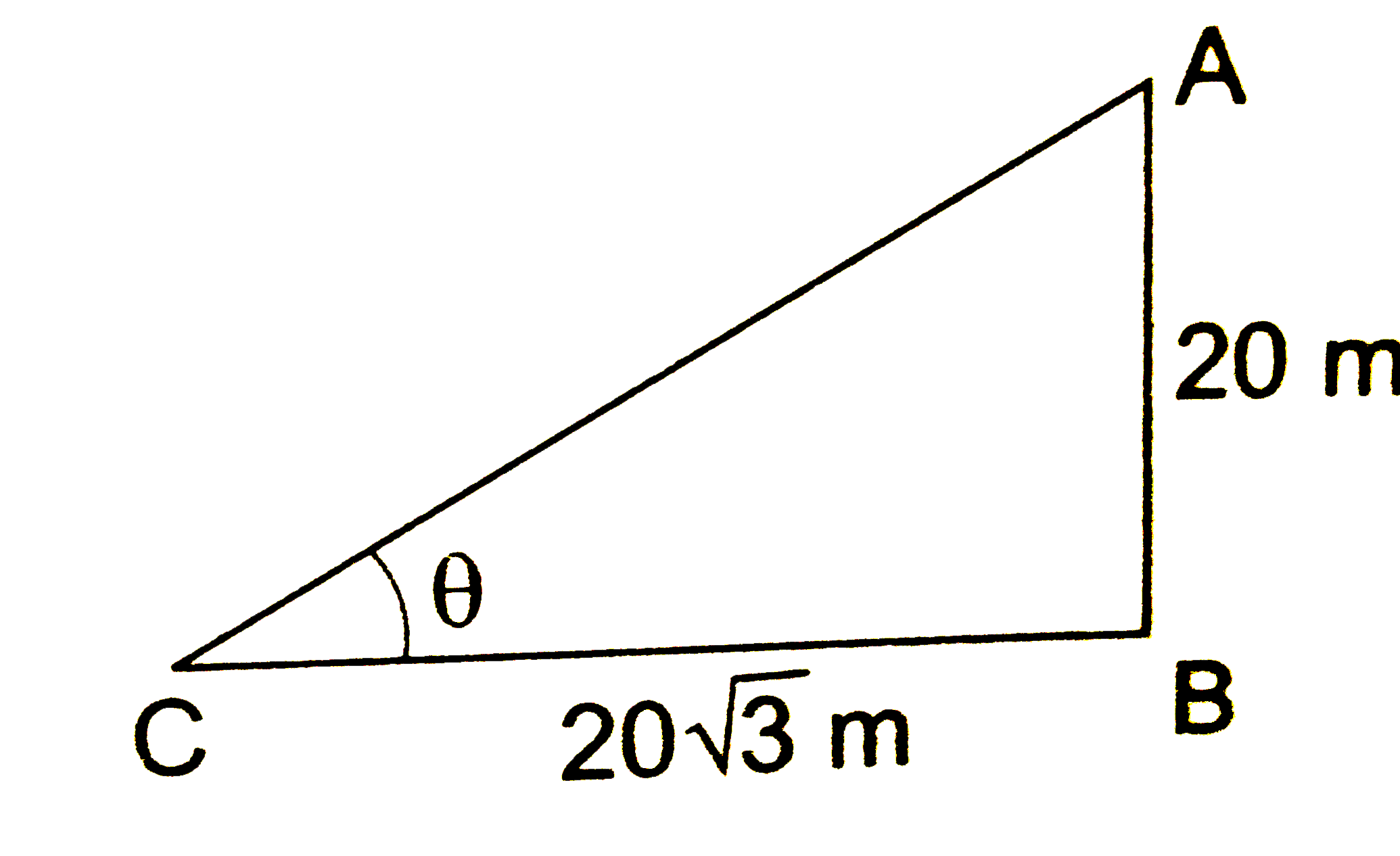
In the following figure, a tower AB is 20 m high and BC, its shadow on the ground, is $20 \sqrt{3}$ m long. Find the Sun’s altitude.

A

$30^{\circ}$

B

$45^{\circ}$

C

$60^{\circ}$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let $A B = 20 m$ be the tower and $B C = 20 \sqrt{3} m$ be the length of the its shadow. Let $∠ A C B = θ$ .
Then, $tan θ = \frac{A B}{A C} = \frac{20}{20 \sqrt{3}} = \frac{1}{\sqrt{3}} = {tan 30}^{\circ}$ .

Updated on:21/07/2023

|

Class 10 MATHS SOME APPLICATIONS OF TRIGONOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

If a pole 12 m high casts a shadow $4 \sqrt{3} m$ long on the ground then the sun's elevation is
A $60^{\circ}$
B $45^{\circ}$
C $30^{\circ}$
D $90^{\circ}$

RS AGGARWAL-HEIGHTS AND DISTANCES-Multiple Choice Questions (Mcq)

Home
Ask Doubt
Profile