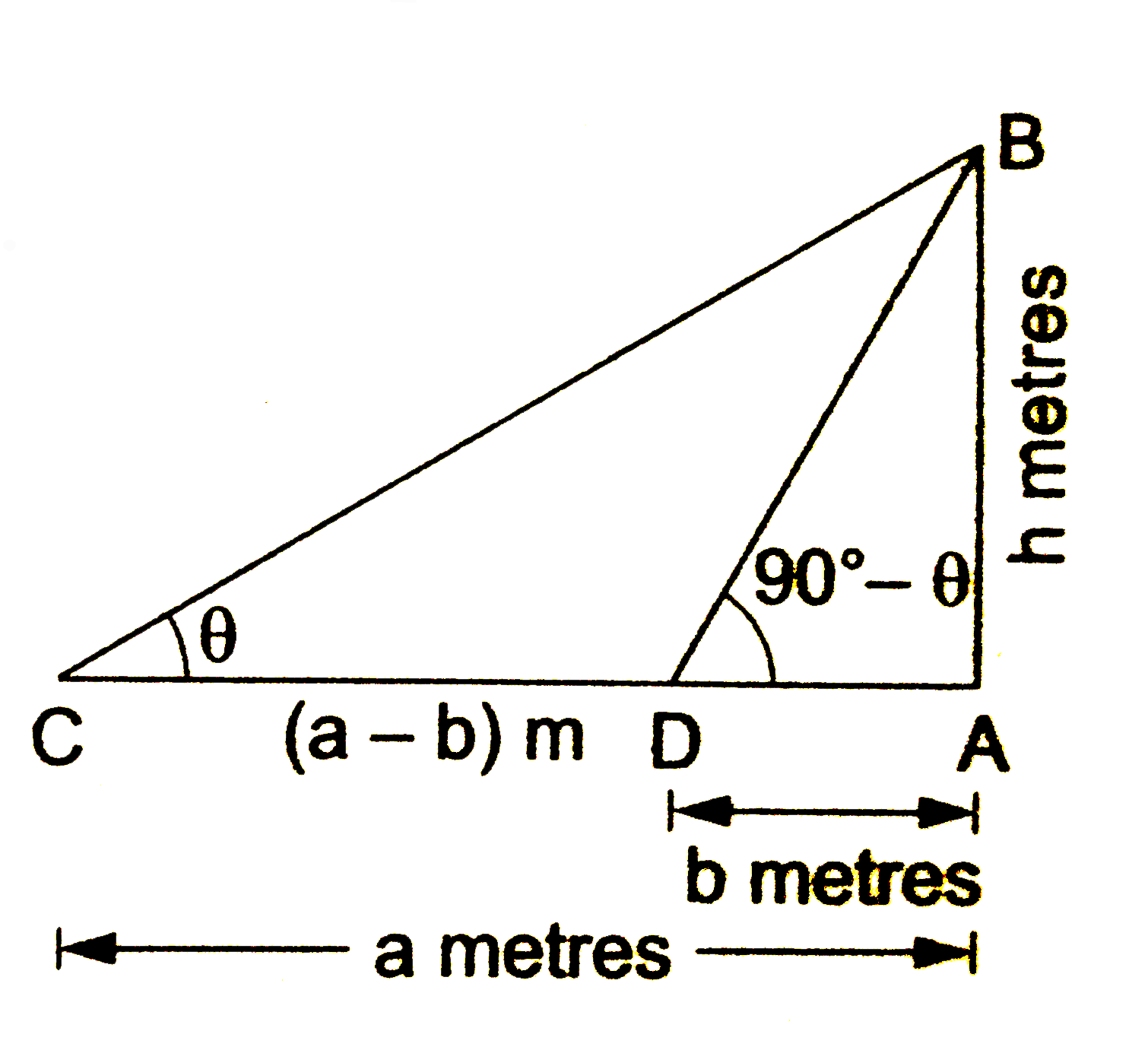
The angle of elevation of the top of a tower from two points on the ground at distances a metres and b metres from the base of the tower and in the same straight line are complementary.Prove that height of the tower is $\sqrt{a b}$ .

Video Solution

Text Solution

Verified by Experts

Let AB be the tower and let C and D be the two positions of the observer. Then,
$A C =$ metres and $A D = b$ metres.
Let $∠ A C B = θ$ . Then, $∠ A D B = (90^{\circ} - θ)$ .
Let $A B = h$ meters.
From right $Δ D A B$ , we have
$\frac{A B}{A D} = tan (90^{\circ} - θ) \Rightarrow \frac{h}{b} = cot θ$
$\Rightarrow h = b tan θ .......... (i)$ .
From right $Δ C A B$ , we have
$\frac{A B}{A C} = tan (90^{\circ} - θ) \Rightarrow \frac{h}{b} = cot θ .......... (i i)$
From (i) and (ii), we get $h^{2} = a b \Rightarrow h = \sqrt{a b}$ .
Hence, the height of the tower is $\sqrt{a b}$ metres.
.

Updated on:21/07/2023