The angle of elevation of a jet plane from a point A on the grund is 600 . After and flight of 30 seconds, the angle of elevation changes to 300. If the jet plane is flying at a constant height of 3600√3m, find the speed of the jet plane.
Let A be the point of observation and let AX be a horizontal line through A and QC⊥AX. Let P and Q bethe two position of the plane. Let PB⊥AX.
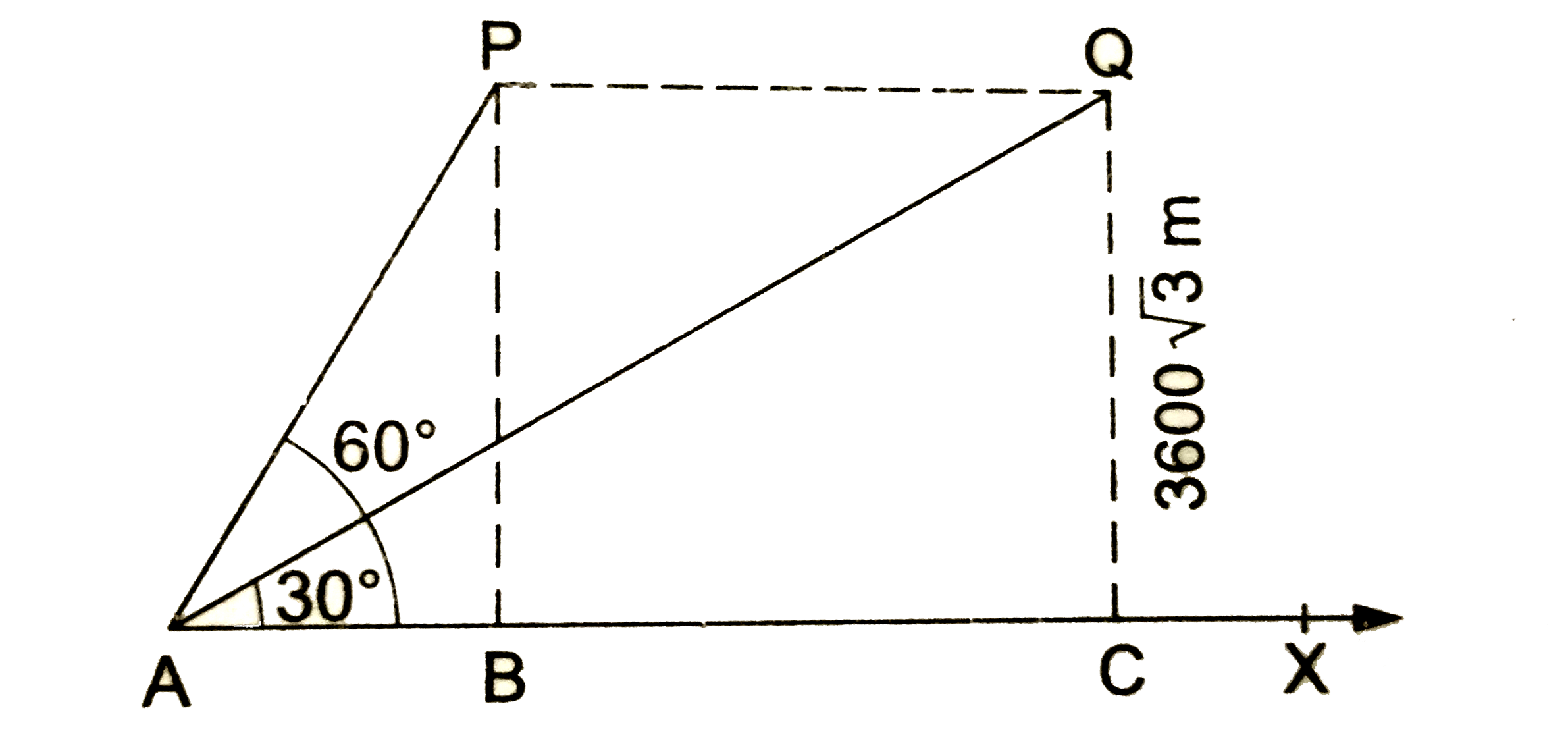
then , PB=QC=3600√3m,∠BAP=60∘ and ∠BAQ=30∘.
From right ΔABP, we have
ABBP=cot60∘=1√3⇒AB3600√3m=1√3
:Et BC=PQ=x metres.
Then, AC=AB+BC=(x+3600)m [using (i) ].
From right ΔACQ , we have
ACCQ=cot30∘=√3⇒x+36003600√3=√3
⇒x+3600=(3600×3)=10800.
⇒x=10800−3600=7200.
Thus , PQ=720metres.
Now, 7200 m is covered in 30 seconds.
∴speed of the jet plane =(720030×60×601000)km/hr
=864km/hr.
Hence, the speed of the jet plane is 864km/hr.
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Exercise 14
38 Videos
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
34 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION
2 Videos
Similar Questions
The angle of elevation of a jet plane from a point A on the grund is 600 . After and flight of 30 seconds, the angle of elevation changes to 300. If the jet plane is flying at a constant height of 3600√3m, find the speed of the jet plane.
View SolutionThe angle of elevation of a jet plane from a point A on the ground is 60o . After a flight of 30 seconds, the angle of elevation changes to 30o . If the jet plane is flying at a constant height of 3600√3m , find the speed of the jet plane.
View Solution
Knowledge Check
The angle of elevation of an airplane from a point on the ground is 60∘. After a flight of 30 seconds, the angle of elevation becomes 30∘. If the airplane is flying at a constant height of 3000√3m, find the speed of the airplane.
A200m/sB250m/sC350m/sD300m/sThe angle of elevation of an aeroplane from a point on the ground is 60∘ .After flying for 30 seconds ,the angle of elevation changes to 30∘ .If the aeroplane is flying at a height of 1500√3 metre , then what is the speed (in m/s) of aeroplane?
A50B100C200D300The angle of elevation of a jet plane from a point A on the ground is 60∘. After a flight of 20 seconds at the speed of 432 km/hour, the angle of elevation changes to 30∘. If the jet plane is flying at a constant height, then its height is :
A1800√3 mB3600√3 mC2400√3 mD1200√3
The angle of elevation of an aeroplane from a point P on the ground is 60∘. After a flight of 15 seconds, the angle of elevation changes to 30∘. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the aeroplane
View SolutionThe angle of elevation of a jet plane from a point A on the ground is 60∘. After a flight of 15 seconds, the angle of elevation changes to 30∘. If the jet plane is flying at a constant height of 1500√3 meter, find the jet plane. (√3=1.732)
View SolutionThe angle of elevation of an aeroplane from a point P on the ground is 60°. After a flight of 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a constant height of 15003 m, find the speed of the aeroplane.
View SolutionThe angle of elevation of the top of a building from the foot of the tower is 60∘. After a flight of 15 seconds, the angle of elevation changes to 30∘. If the aeroplane is flying at a constant height of 1500√3m find the speed of the plane in km/hr.
View SolutionThe angle of elevation of an aeroplane from a point on the ground is 60∘ . After flying for 30 seconds, the angle of elevation charges to 30∘ . If the aeroplane is flying at a height of 4500 m, then what is the speed (in m/s) of aeroplane
View Solution