From the top of a light house, the angles of depression of two ships on the opposite sides of its are observed to be $α a n d β$ . If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is $(h \frac{tan α + tan β}{tan α t a n β}$

Video Solution

Text Solution

Verified by Experts

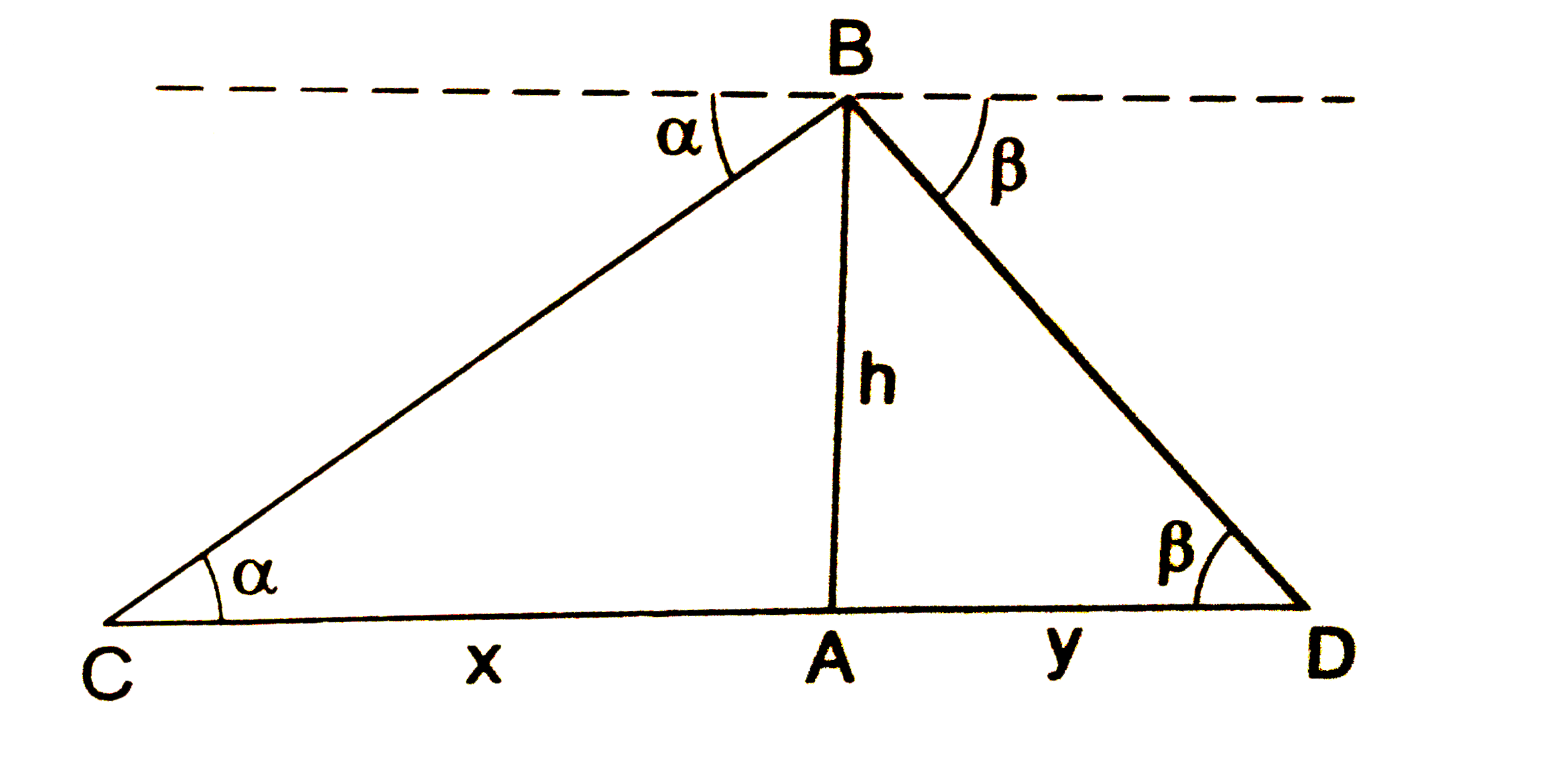
Let AB be the lighthouse and C and D be the positions of the two ships. Then, $A B = m$ metres.
Clearly, $∠ A C B = α$ and $∠ A D B = β$ .
Let $A C = x$ metres and
$A D = y$ metres.
From right $Δ C A B$ , we have
$\frac{A C}{A B} = cot α \Rightarrow \frac{x}{h} = cot α \Rightarrow x = h cot α . ........... (i)$
From right $Δ D A B$ , we have
$\frac{A D}{A B} = cot β \Rightarrow \frac{y}{h} = cot β \Rightarrow y = h cot β .......... (i)$
Adding the corresponding sides of (i) and (ii), we get
$x + y = h (cot α + cot β) = h (\frac{1}{tan α} + \frac{1}{tan β})$
$\Rightarrow x + y = \frac{h (tan α + tan β)}{tan α tan β}$
Hence the distane between the ships is $\frac{h (tan α + tan β)}{tan α tan β} m$ .

Updated on:21/07/2023