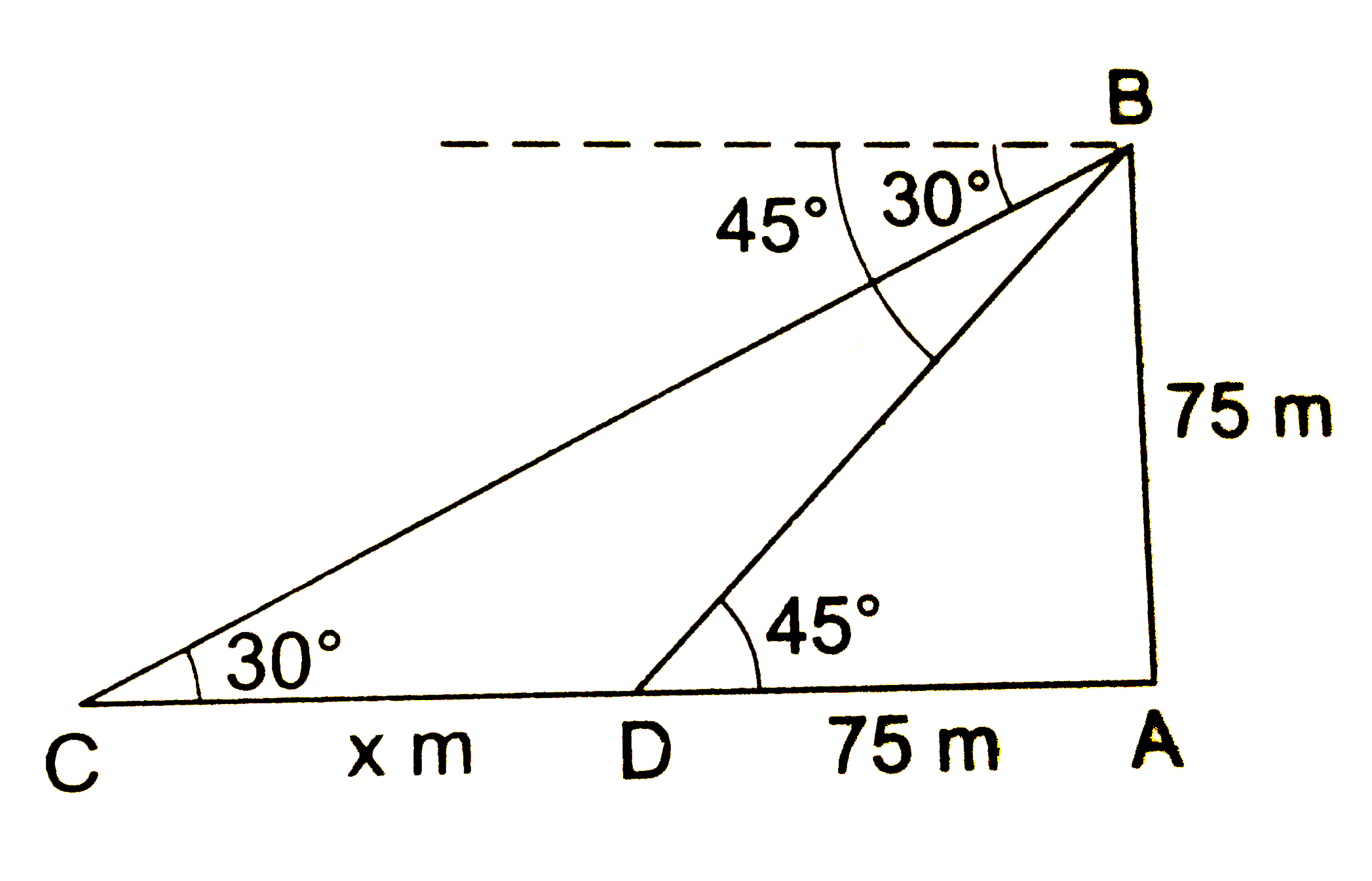
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30o and 45o . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two sh
Let AB be the lighthouse and C and D be the positions of two ships. Then ,
AB=75m,∠ACB=30∘,
and ∠ADB=45∘.
Let CD = x metres.
From right ΔDAB, we have
ADAB=cot45∘=1
⇒ADAB=cot45∘=1
⇒AD75m=1⇒AD=75m.
From right ΔCAB , we have
CAAB=cot30∘=√3⇒x+7575=√3
⇒x+75=75√3⇒x=75(√3−1)=75(1.73−1)
⇒x=(75×0.73)=54.75.
Hence, the distance between the ships is 54.75 metres.
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Exercise 14
38 Videos
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
34 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION
2 Videos
Similar Questions
As observed from the top of a 100 m high lighthouse from the sea level, the angles of depression of two ships are 30∘ and 45∘ If one ship is exactly behind the other one on the same side of the lighthouse, find the distance between the two ships.
View SolutionAs observed from the top of a 75m tall lighthouse, the angles of depression of two ships are 30o and 45o . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
View Solution
Knowledge Check
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30∘and 45∘. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A75(√3−1)mB85(√3−1)mC75(√3+1)mDNoneFrom the top of a lighthouse. 100 m high, the angle of depression of two ships are 30° and 45°, if both ships are on same side find the distance between the ships ?
AA. 120 mBB. 180 mCC. 240 mDD. 360 mFrom the top of a light -house at a height 20 metres above sea -level,the angle of depression of a ship is 30∘.The distance of the ship from the foot of the light house is
A20 mB20√3mC30 mD30√3m
As observed from the top of a 150 m tall light house, the angles of depression of two ships approaching it are 30o and 45o . If one ship is directly behind the other, find the distance between the two ships.
View SolutionAs observed from the top of a light house, 100 m high above sea level, the angles of depression of a ship, sailing sirectly towards it, changes from 30∘ and 90∘.
View SolutionTwo ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships are observed from the top of the light house are 60o and 45o respectively. If the height of the light house is 200 m, find the distance between the two ships. (Use √3=1.73)
View SolutionFrom a lighthouse the angles of depression of two ships on opposite sides of the light-house are observed to be 30∘and45∘ If the height of lighthouse is h, what is the distance between the ships
View SolutionFrom a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30∘and45∘ If the height of the light house is h metres, the distance between the ships is
View Solution
