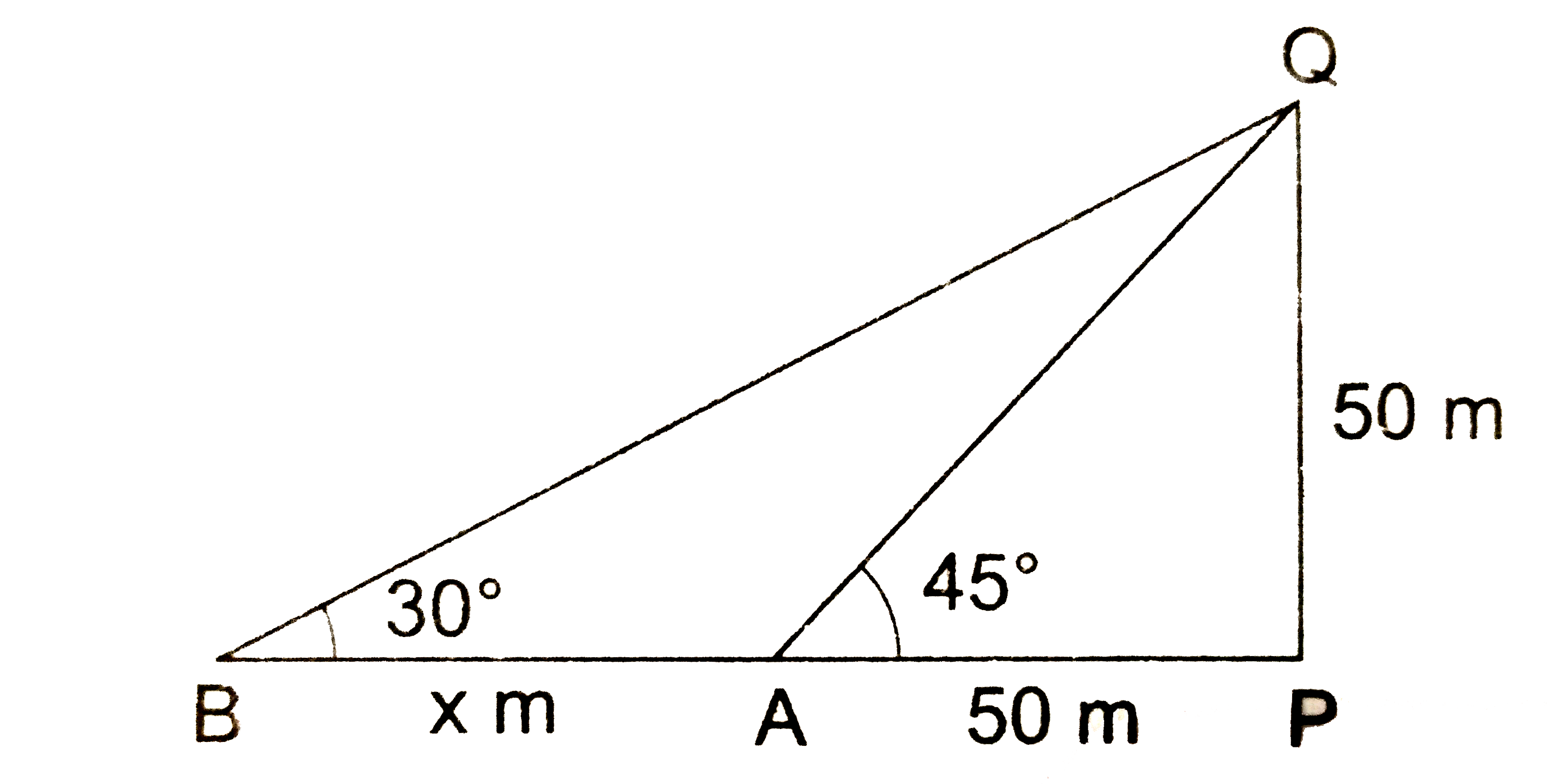
A tower is 50 m high. Its shadow is x metres shorter when the sun's altitude is 45∘ than when it is 30∘. Find the value of x correct to nearest cm.

A

36.6 m

B

32.5 m

C

30.5 m

D

31.5 m

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Let PQ be the tower and let PA and PB be its shadows whenm the altitudes of the sun are 45∘ and 30∘ respectively. Then,
∠PAQ=45∘,∠PBQ=30∘,∠BPQ=90∘,PQ=50m.
Let AB=x metres.
From right ΔAPQ, we have
APPQ=cot45∘=1
⇒APBQ=cot30∘=√3⇒x+5050=√3⇒x=50(√3−1).
⇒x=50(1.732−1)=(50×0.732)=36.6
Hence, x=36.6
ocr_image

Updated on:21/07/2023
|
Class 10MATHSSOME APPLICATIONS OF TRIGONOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The shadow of a tower standing on a level plane is found to be 40 m longer when the sun 's altitude is 45∘ , than when it is 60∘ . The height of the tower is

    A30(3+√3) metre
    B40(3+√3) metre
    C20(3+√3) metre
    D10(3+√3) metre

  • The shadow of a tower standing on a level plane is found to be 50m longer when sun's altitude is 30∘ then when it is 60∘. Find the height of tower.

    A40.3m
    B43.3m
    C43.9m
    D46.3m