$(6, 0), (0, 6) and (7, 7)$ are the vertices of a triangle. The circle inscribed in the triangle has the equation

A

$x^{2} + y^{2} - 9 x - 9 y + 36 = 0$

B

$x^{2} + y^{2} + 9 x - 9 y + 36 = 0$

C

$x^{2} + y^{2} + 9 x + 9 y - 36 = 0$

D

$x^{2} + y^{2} + 18 x - 18 y + 36 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

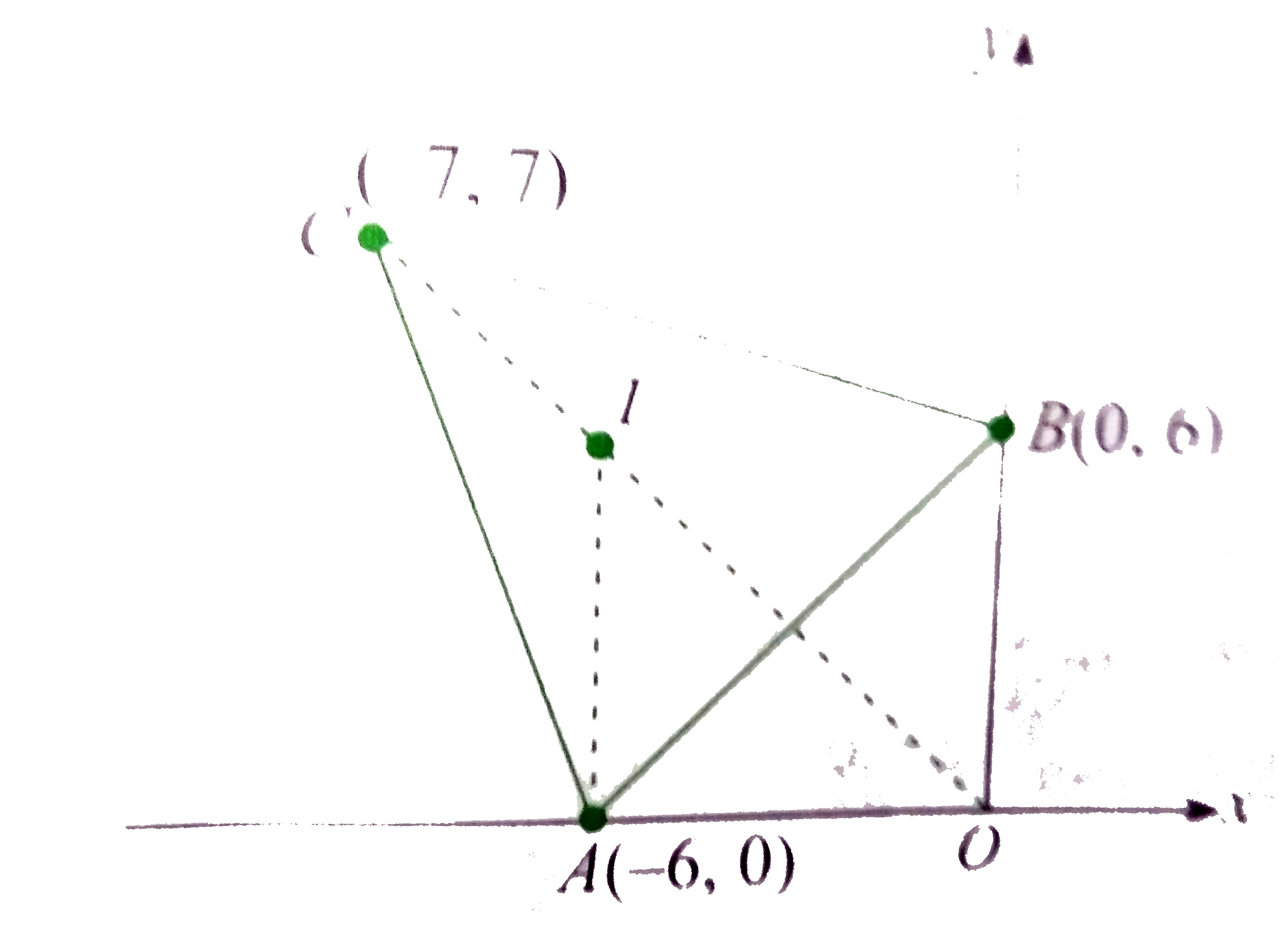
The triangle is evidently isosceles and, therefore, the median through C is the angle bisector of $∠ C$ .
The equation of the angle bisector is $y = - x$ and the incenter
$I \equiv (- a, a)$ where a is positive.
The equation of AC is $y - 0 = - 7 (x + 6), i . e ., 7 x + y + 42 = 0$
and the equation of AB is $x - y + 6 = 0$ .
The lengths of the perpendiculars from I to AB and AC are equal. Therefore,
$∣ ∣ ∣ \frac{- 7 a = a + 42}{\sqrt{50}} ∣ ∣ ∣ = ∣ ∣ ∣ \frac{- a - a + 6}{\sqrt{2}} ∣ ∣ ∣$
or $a = \frac{9}{2}$ $(∵ a > 0)$
Therefore, the center is $(- 9 / 2, 9 / 2)$ and the radius is $3 / \sqrt{2}$ .
Hence, the equation of the circle is
${(x + \frac{9}{2})}^{2} + {(y - \frac{9}{2})}^{2} = \frac{9}{2}$
or $x^{2} + y^{2} + 9 x - 9 y + 36 = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Points A(6,6) ,B(2,3) and C(4,7) are the vertices of a triangle which is :
Aright angled
Bacute angled
Cobtuse angled
Dnone of the above
Question 2 - Select One
Points A(6,6) ,B(2,3) and C(4,7) are the vertices of a triangle which is :
Aright angled
Bacute angled
Cobtuse angled
Dnone of these
Question 3 - Select One
The vertices of a triangle ABC are the points (6,0),(0,6) and (7,7). The equation of the circle inscribed in the triangle is
A $x^{2} + y^{2} - 9 x - 9 y + 36 = 0$
B $x^{2} + y^{2} - 9 x - 9 y - 36 = 0$
C $x^{2} + y^{2} - 9 x + 9 y + 36 = 0$
D $x^{2} + y^{2} + 9 x - 9 y + 36 = 0$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile