A variable chord of circle x2+y2=4 is drawn form the point P (3,5)meeting the circle at the point A and B. A point Q is taken on this chord such that 2PQ=PA+PB. Locus of point 'Q' is
x2+y2+3x+4y=0
x2+y2=36
x2+y2=16
x2+y2−3x−5y=0
The correct Answer is:4
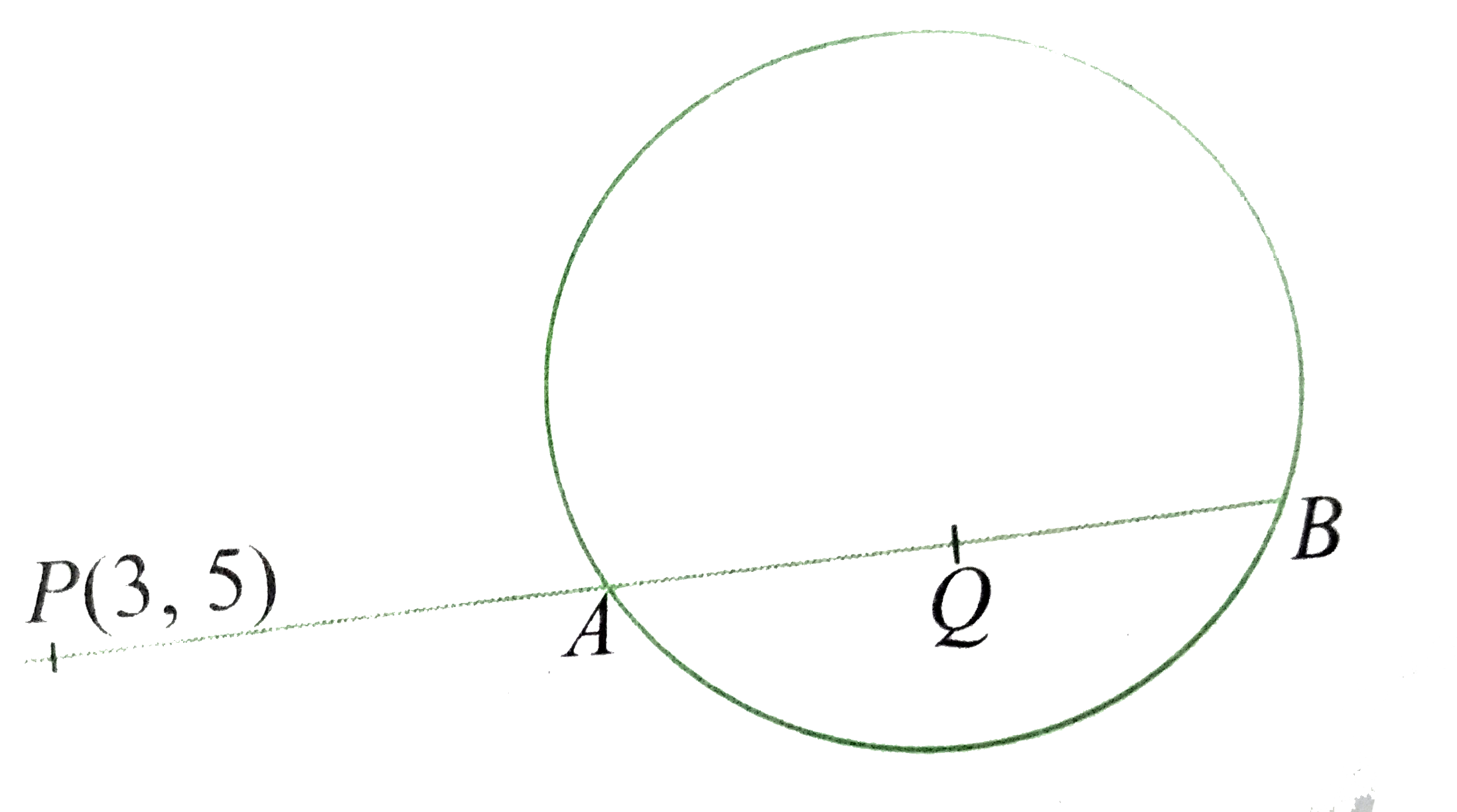
2PQ=PA+PB
or PQ−PA=PB−PQ
or AQ=QB
Therefore, Q is the midpoint of AB.
Let Q has coordinates (h,k).
Then the equation of chord AB is given by T=S1
or hx+ky−4=h2+k2−4
This variable chord passes through the point P(3,5). Therefore,
3h+5k=h2+k2
or x2+y2−3x−5y=0
which is the required locus.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
A variable chord of the circle x2+y2=4 is drawn from the point P(3,5) meeting the circle at the point A and B. A point Q is taken on the chord such that 2PQ=PA+PB . The locus of Q is x2+y2+3x+4y=0 x2+y2=36 x2+y2=16 x2+y2−3x−5y=0
View SolutionA line drawn through the point P(4,7) cuts the circle x2+y2=9 at the points A and B .Then PA.PB is equal to:
View Solution
Knowledge Check
Chord of the circle x2+y2=81 bisected at the point (−2,3) meets the diameter x+5y=0 at a point
Aon the ciecleBinside the circleCoutside the circleDnone of theseA line is drawn through the point P(3,11) to cut the circle x2+y2=9 at A and B. Then, PA⋅PB is equal to
A9B121C205D139A line is drawn through the point P(3,11) to cut the circle x2+y2=9 at A and B. Then PA.PB is equal to
A9B121C205D139
A variable chord of circle x2+y2+2gx+2fy+c=0 passes through the point P(x1,y1). Find the locus of the midpoint of the chord.
View SolutionA variable chord is drawn through the origin to the circle x2+y2−2ax=0 . Find the locus of the center of the circle drawn on this chord as diameter.
View SolutionThe locus of the centers of the circles such that the point (2, 3) is the mid point of the chord 5x+2y=16 is
View SolutionLet P be the point (1,0) and Q a point on the locus y2=8x. The locus of mid-point of PQ is :
View SolutionPQ is a chord of the circle x2+y2−2x−8=0 whose mid-point is (2, 2). The circle passing through P, Q and (1, 2) is
View Solution