The circle which can be drawn to pass through (1, 0) and (3, 0) and to touch the y-axis intersect at angle θ. Then cosθ is equal to 12 (b) −12 (c) 14 (d) −14
A
1/2
B
1/3
C
1/4
D
−1/4
Video Solution
Text Solution
The correct Answer is:1
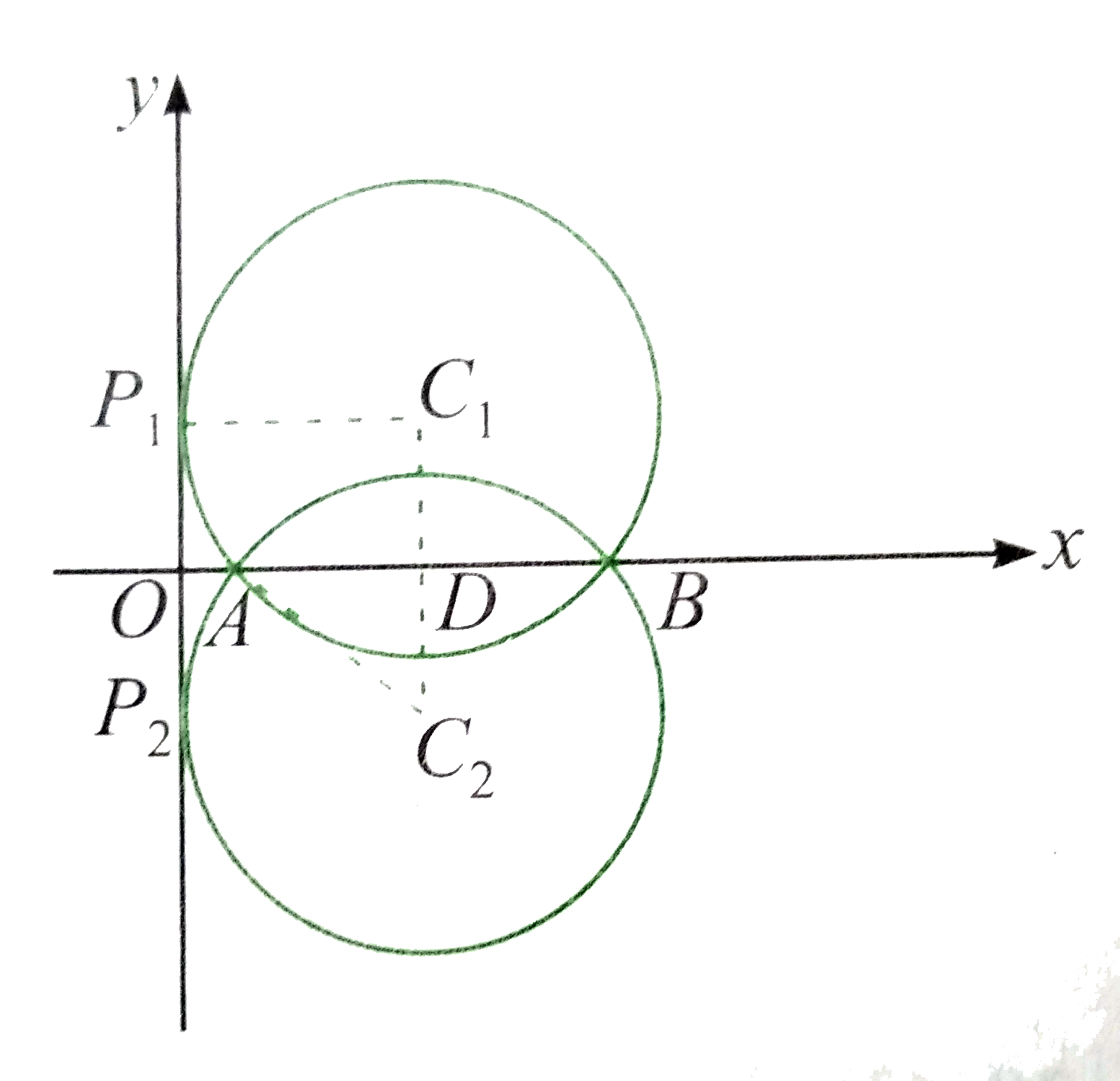
Let A≡(1,0),B≡(3,0) and C1 and C2 be the centers of circles passing through A and Band touching the y-axis at P1 and P2 respectively. If r is the radius ( here radii of both circles will be the same ).
C1A=C2A=r=OD=2
and C1=(2,h)
or C1≡(2,√3),C2≡(2,−√3)
If ∠C1AC2=θ, then
cosθ=AC21+AC22−C1C222AC1×AC2=12
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)46videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.65videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank31videos
BINOMIAL THEORM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank32videos
CIRCLES
Similar Questions
Knowledge Check
- Question 1 - Select One
The circles which can be drawn to pass through (3,0) and (5,0) and to touch the y-axis intersect at an angle θ , then cosθ is equal to
A7/8B1/2C0Dnone of these - Question 2 - Select One or More
Equations of circles which pass through the points (1,-2) and (3,-4) and touch the x-axis is
Ax2+y2+6x+2y+9=0Bx2+y2+10x+20y+25=0Cx2+y2−6x+4y+9=0Dnone - Question 3 - Select One
The centre of the circle passing through (0, 0) and (1, 0) and touching the circle x2+y2=9, is
A(3/2, 1/2)B(1/2, 3/2)C(1/2, 1/2)D(1/2,±√2)
Two circles are drawn through the points (a,5a)and(4a,a) to touch the y-axis. Prove that they intersect at angle tan−1(409).
View SolutionFind the equation of circle passing through the points (1,-2) and (3,-4) and touches the X-axis.
View SolutionThe radius of the tangent circle that can be drawn to pass through the point (0, 1) and (0, 6) and touching the x-axis is(a) 5/2 (b)Â 3/2 (c) 7/2 (d) 9/2
View SolutionThe circle passing through the point (-1,0) and touching the y-axis at (0,2) also passes through the point:
View SolutionThe circle passing through (1,-2) and touching the X-axis at (3 ,0) , also passes through the point
View Solution

