Through the point P(3,4) a pair of perpendicular lines are dranw which meet x-axis at the point A and B. The locus of incentre of triangle PAB is
x2−y2−6x−8y+25=0
x2+y2−6x−8y+25=0
x2−y2+6x+8y+25=0
x2+y2+6x+8y+25=0
The correct Answer is:1
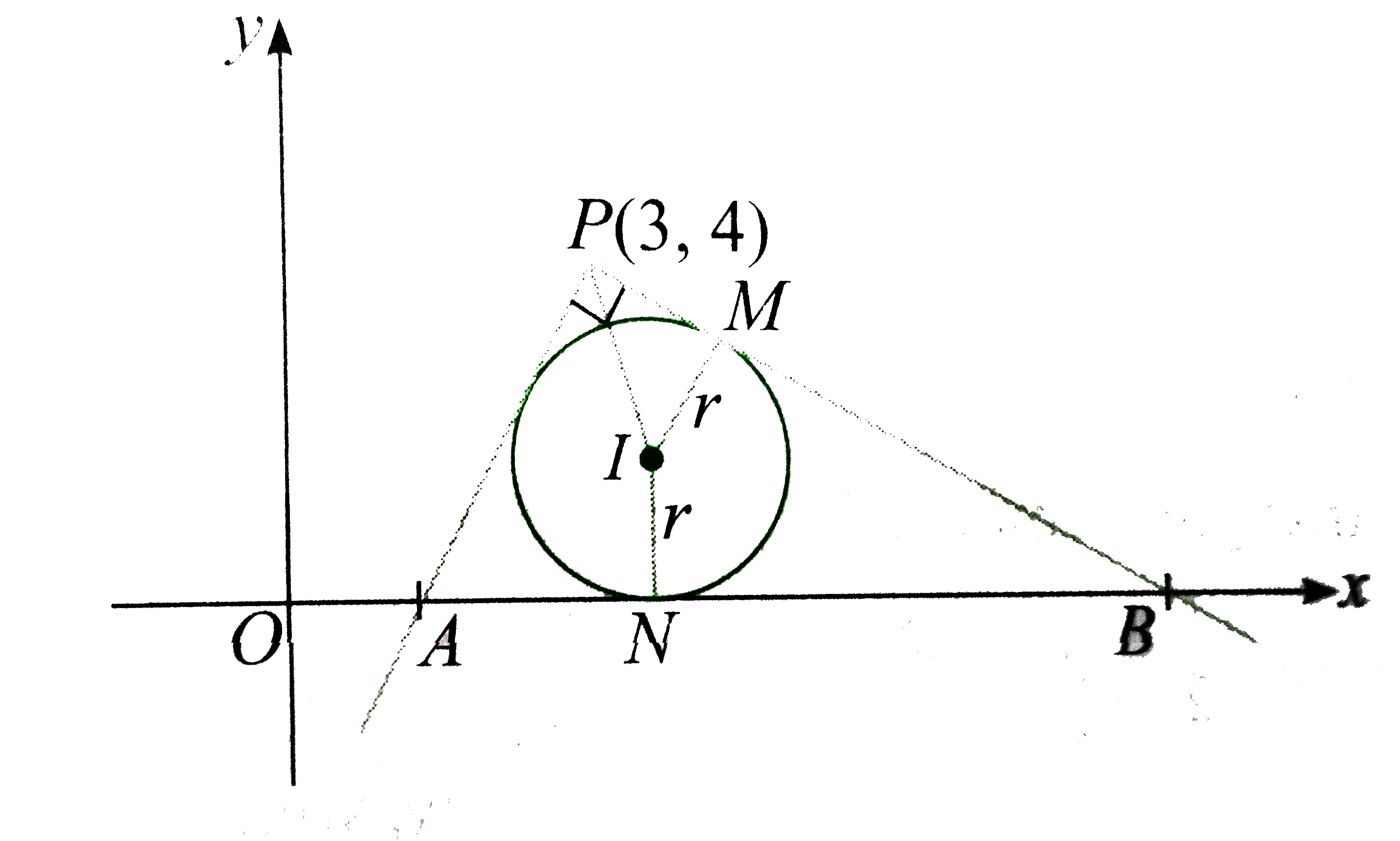
Let point I be (h,k).
From the figure,
IP=rcosec45∘, where r= inradius
⇒(IP)2=2r2
⇒(3−h)2+(4−k)2=2(|k|)2
( As circle touches x-axis, r=(|k|)2
⇒x2−y2−6x−8y+25=0, which is the require locus.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
" The line "4x+3y=-12" meets x-axis at the point "
View SolutionA curve is defined parametrically be equations x=t2andy=t3 . A variable pair of perpendicular lines through the origin O meet the curve of PandQ . If the locus of the point of intersection of the tangents at PandQ is ay2=bx−1, then the value of (a+b) is____
View Solution
Knowledge Check
Through point P(−1,4), two perpendicular lines are drawn which intersect x-axis at Q and R. find the locus of incentre of ΔPQR.
Ax2+y2+2x−8y−17=0Bx2−y2+2x−8y+17=0Cx2+y2−2x−8y−17=0Dx2−y2+8x−2y−17=0A pair of perpendicular lines passing through P(1.4) intersect x-axis at Q and R, then the locus of incentre of ΔPQR is
Ax2+y2−2x−8y+17=0Bx2+y2+2x−8y+17=0Cx2−y2−2x−8y+17=0Dx2+y2−2x+8y+17=0Tangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at points A and B. The orthocenter of the △PAB is
A(5,87)B(75,258)C(115,85)D(825,75)
the lines 3x + 4y 12 and Consider a variable line L which passes through the point of intersection P of x + 2y-5 = 0 meeting the coordinate axes at points A and B. Then 5 4. · locus of middle point°f segment AB has the equation豆+x-4 2(x2 + y2) = 4x + 3y locus of centroid of the variable triangle OAB has the equation (where O is origin)-+-6 (A) (B) locus of the feet of the perpendicular from the origin on the variable line L has the equation (C) (D) locus of middle point of segment AB has the equation 8 3
View SolutionTangents are drawn from the point P(3, 4) to the ellipse x29+y24=1 touching the ellipse at points A and B. The orthocenter of the triangle PAB is
View SolutionIf the point 3x+4y−24=0 intersects the X-axis at the point A and the Y-axis at the point B, then the incentre of the triangle OAB, where O is the origin, is
View SolutionA variable straight line drawn through the point of intersection of lines xa+yb=1 and xb+ya=1 meets the co ordinates axes in A and B. Locus of the mid point of AB is ……….
View SolutionTangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at points A and B. The orthocentre of ΔPAB, is
View Solution