If one of the diameters of the circle x2+y2−2x−6y+6=0 is a chord to the circle with centre (2, 1), then the radius of circle is:
√3
√2
3
2
The correct Answer is:3
The given circle is x2+y2−2x−6y+6=0
Its center is H(1,3) and radius is 2.
AH=2
Radius of the required circle =AC
=√AH2+CH2=√22+5=3
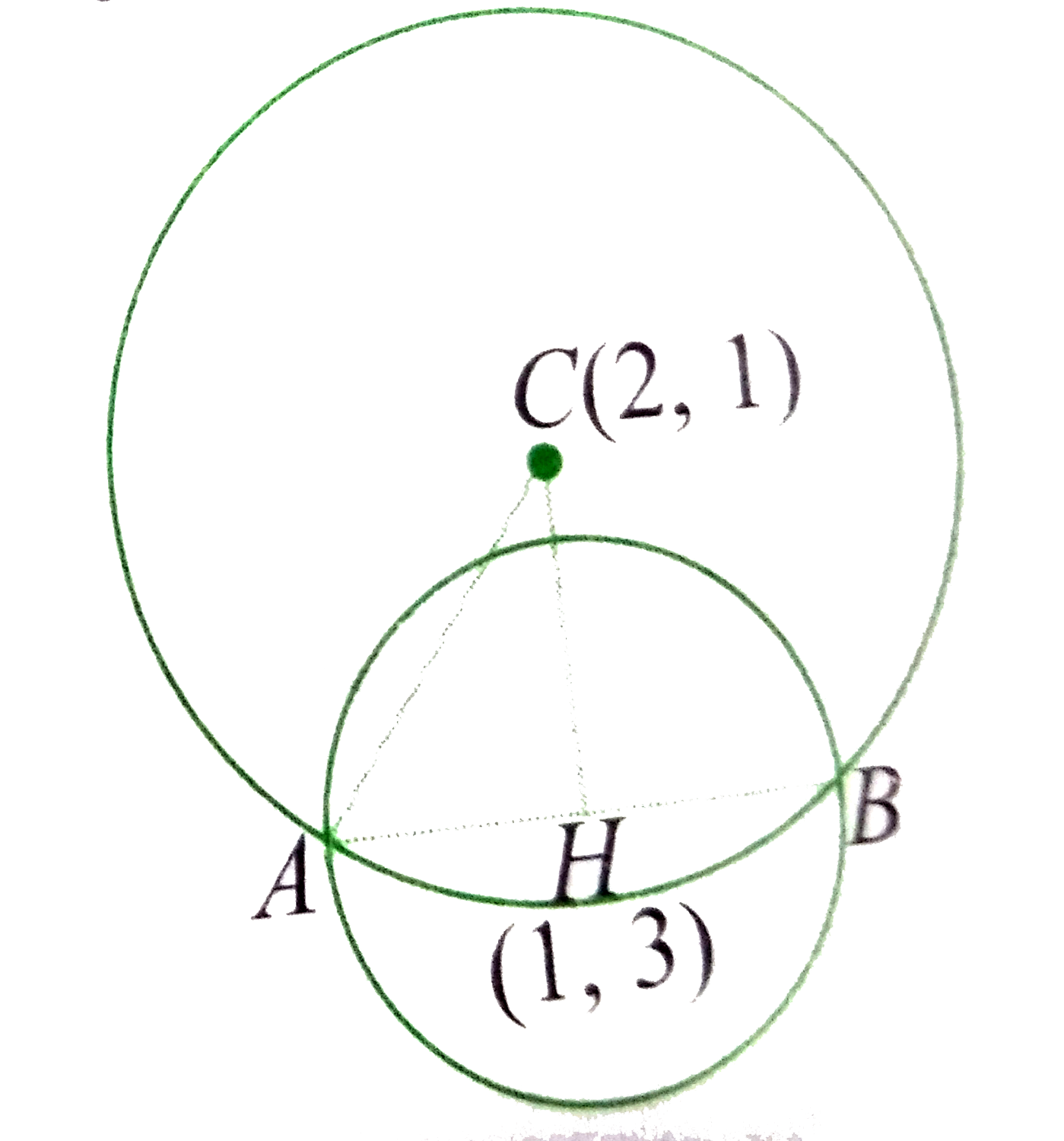
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
If one of the diameters of the circle x2+y2−2x−6y+6 =0 is a chord to the circle with centre at (2,1) then the radius of the circle is equal to.
View SolutionIf one of the diameters of the circle x2+y2−2x−6y+6=0 is a chord to the circle with center (2,1) ,then the radius of the circle is
View Solution
Knowledge Check
A diameter of x2+y2−2x−6y+6=0 is a chord to circle centre (2, 1), then radius of the circle is
A1B2C3D4If one end of a diameter of the circle 3x2+3y2−9x+6y+5=0 is (1,2), then the other end is
A(2,1)B(2,4)C(2,-4)D(-4,2)If one of the diameter of the circle, given by the equation x2+y2+4x+6y−12=0, is a chord of a circle S, whose centre is (2,-3), the radius of S is
A√41 unitsB3√5 unitsC5√2 unitsD2√5 units
If one of the diameters of the curve 2+y2−4x−6y+9=0 is a chord of a circle with centre (1,1) then the radius of this circel is
View SolutionDiameter of x2+y2−2x−6y+6=0 is chord of circle with center (2,1) then radius of bigger circle is
View SolutionOne of the diameters of the circle x2+y2−12x+4y+6=0 is given by
View SolutionThe length of the diameter of the circle x2+y2−4x–6y+4=0 is -
View SolutionIf one of the diameters of the circle, given by the equation, x2+y2−4x+6y−12=0 , is a chord of a circle S, whose centre is at (−3,2) , then the radius of S is :
View Solution
