A line meets the co-ordinate axes in A and B. A circle is circumscribed about the triangle OAB. If and are the distances of the tangent to the circle at the origin O from the points A and B respectively, the diameter of the circle is:
The correct Answer is:3
Let the circle be .
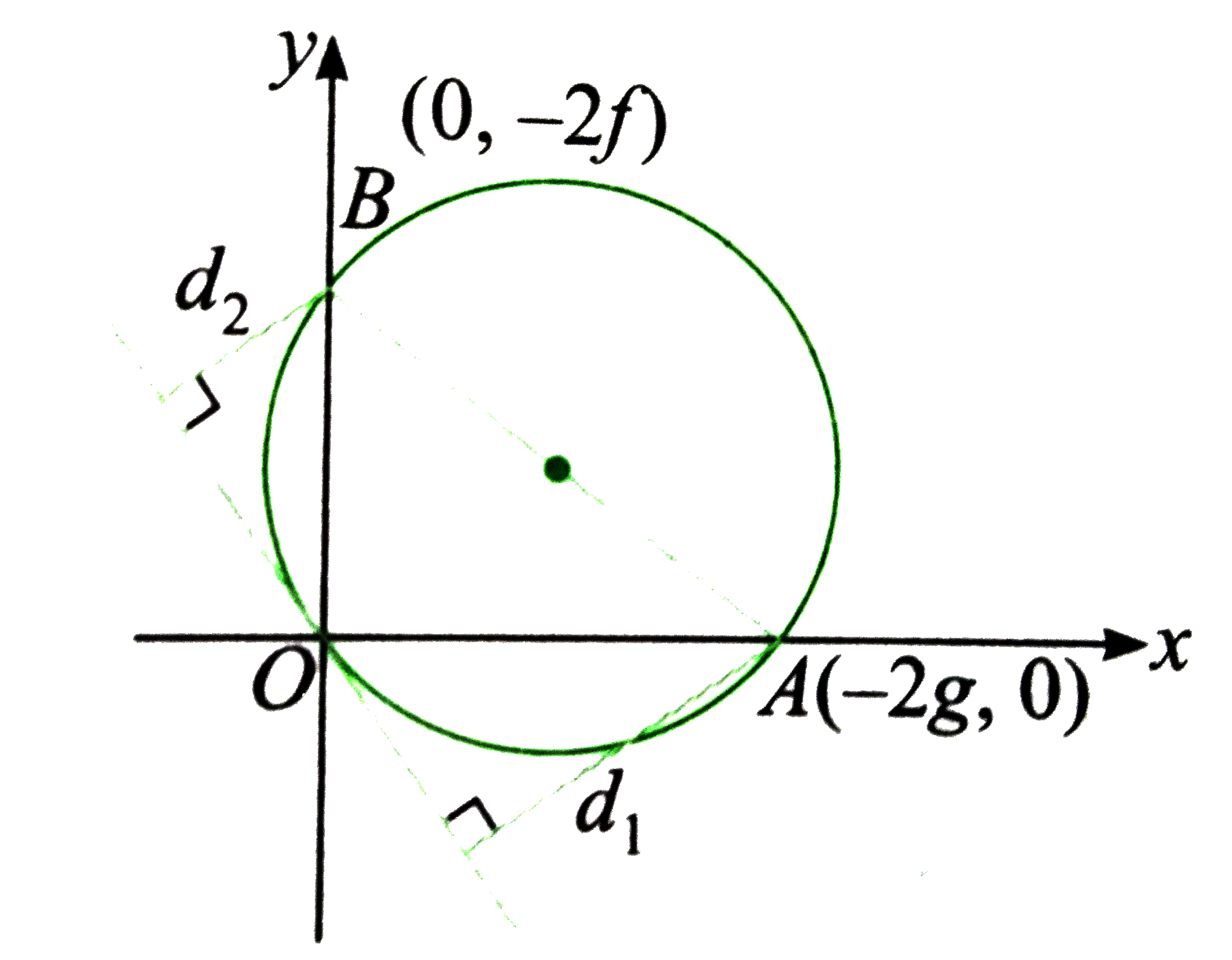
Tangent at the origin is
and
or
Diameter of the circle
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
A line meets the coordinate axes at A and B . A circle is circumscribed about the triangle OAB. If d1andd2 are distances of the tangents to the circle at the origin O from the points AandB , respectively, then the diameter of the circle is 2d1+d22 (b) d1+2d22 d1+d2 (d) d1d2d1+d2
View SolutionA line 2x+y=1 intersect co-ordinate axis at points A and B. A circle is drawn passing through origin and point A & B. If perpendicular from point A and B are drawn on tangent to the circle at origin then sum of perpendicular distance is (A) 5√2 (B) √52 (C) √54 (D) 52
View Solution
Knowledge Check
A line meets the coordinate axes at A and B. A circle is circumscribed obout the triangle OAB. If the distance of the points A and B from the tangent at O, the origin, to the circle are m and n respectively, find the diameter of the circle.
A2m+n2B(m+n)Cmnm+nDm+2n2Aline meets the co-ordinate axes in A and B.A circle is circumscribed about the triangle OAB. The distances from the end points of the side AB to the line touching the circle at the origin O are equal to pand g respectively. The diameter of the circle is
Ap(p+q)Balp+q)Cp+qD12(p+q)A line meets the co-ordinates axes at A(a, 0) and B(0, b) A circle is circumscribed about the triangle OAB. If the distance of the points A and B from the tangent at origin to the circle are 3 and 4 repectively, then the value of a2+b2+1 is
A20B30C40D50
A circle is circumscribed about a right angled triangle ABC right angled at vertex B. Line L .is a tangent to this circle drawn at point B. Length of perpendiculars drawn from vertices A and C upon L are 5 and 8 respectively, then radius of the this circumcircle can be
View SolutionPA and PB are tangents to a circle with centre O from point P. OP is equal to the diameter of the circle. Prove that ABP is equilateral triangle,
View SolutionPoint O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle.

View SolutionA line makes equal intercepts of length a on the coordinate axes. A circle is circumscribed about the triangle which the line makes with the coordinate axes. The sum of the distance of the vertices of the triangle from the tangent to this circle at the origin is
View SolutionThe straight line x + 2y = 1 meets the coordinate axes at A and B. A circle is drawn through A,B and the origin. Then, the sum of perpendicular distances from A and B on the tangent to the circle at the origin is
View Solution
