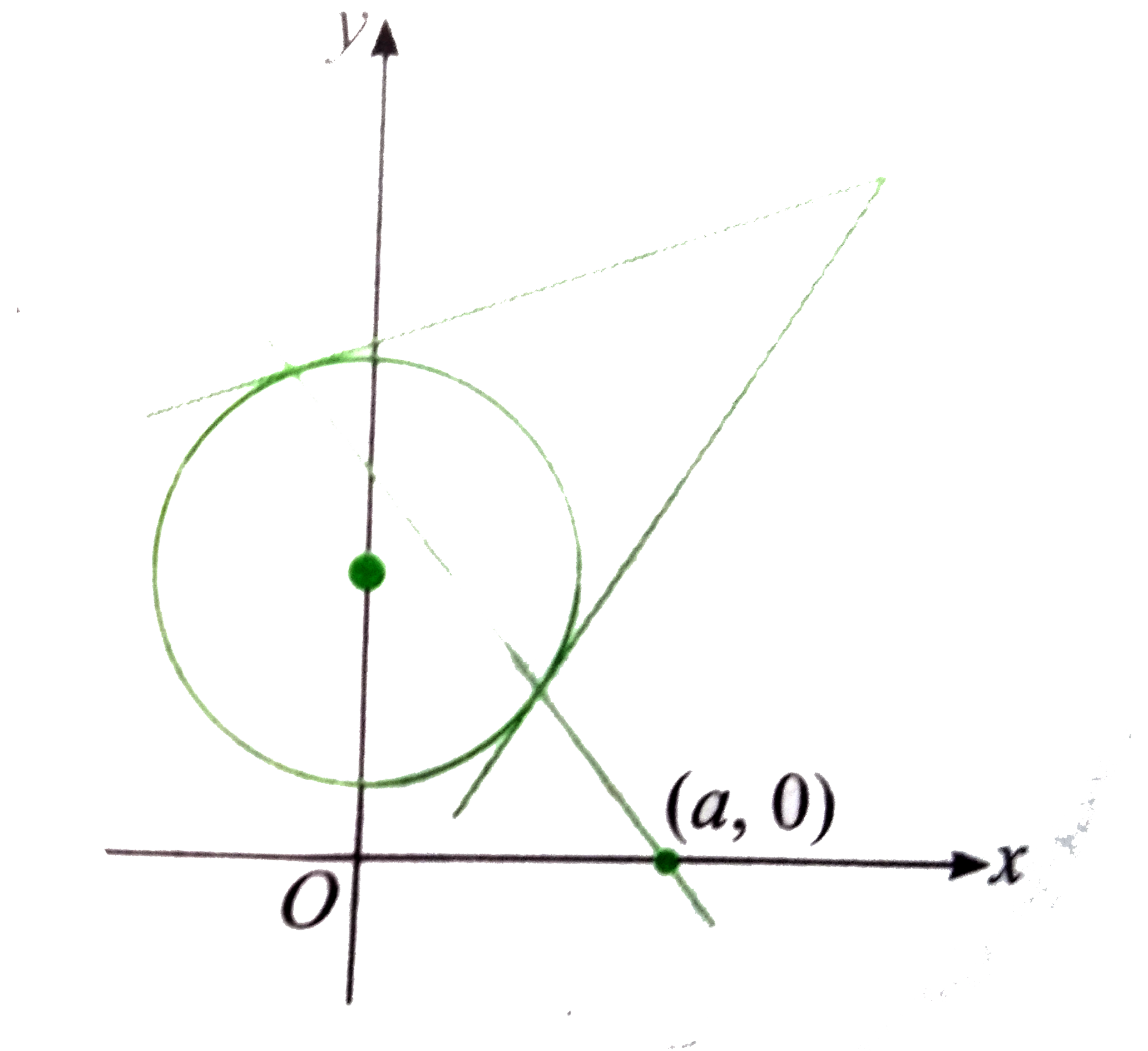
A circle with radius $| a |$ and center on the y-axis slied along it and a variable line through (a, 0) cuts the circle at points $P a n d Q$ . The region in which the point of intersection of the tangents to the circle at points $P$ and $Q$ lies is represented by $y^{2} \geq 4 (a x - a^{2})$ (b) $y^{2} \leq 4 (a x - a^{2})$ $y \geq 4 (a x - a^{2})$ (d) $y \leq 4 (a x - a^{2})$

A

$y^{2} \geq 4 (a x - a^{2})$

B

$y^{2} \leq 4 (a x - a^{2})$

C

$y \geq 4 (a x - a^{2})$

D

$y = 4 (a x - a^{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

Let the center be $(0, α)$ . Then the equation of the circle is $x^{2} + {(y - α)}^{2} = {| a |}^{2}$ .
So, the equation of chord of contact for P(h,k) is $x h + y k - α (y + k) + α^{2} - a^{2} = 0$
It passes through $(a, 0)$ .
Therefore,
$α^{2} - α k + a h - a^{20 = 0}$
As $α$ is real,
$k^{2} - 4 (a h - a^{2}) \geq 0$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

The equation of the circle having centre (0, 0) and passing through the point of intersection of the lines $4 x + 3 y = 2 and x + 2 y = 3$ is
A $x^{2} + y^{2} = \sqrt{5}$
B $x^{2} + y^{2} = 5$
C $x^{2} + y^{2} = 4$
D $x^{2} + y^{2} = 2$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile