If the line is the equation of a transverse common tangent to the circles and , then the value of is (b) (c) (d)
The correct Answer is:3
and
Thus, circle touch each other externally .
The equation of common tangent at P is
(1)
Comparing it with , we get
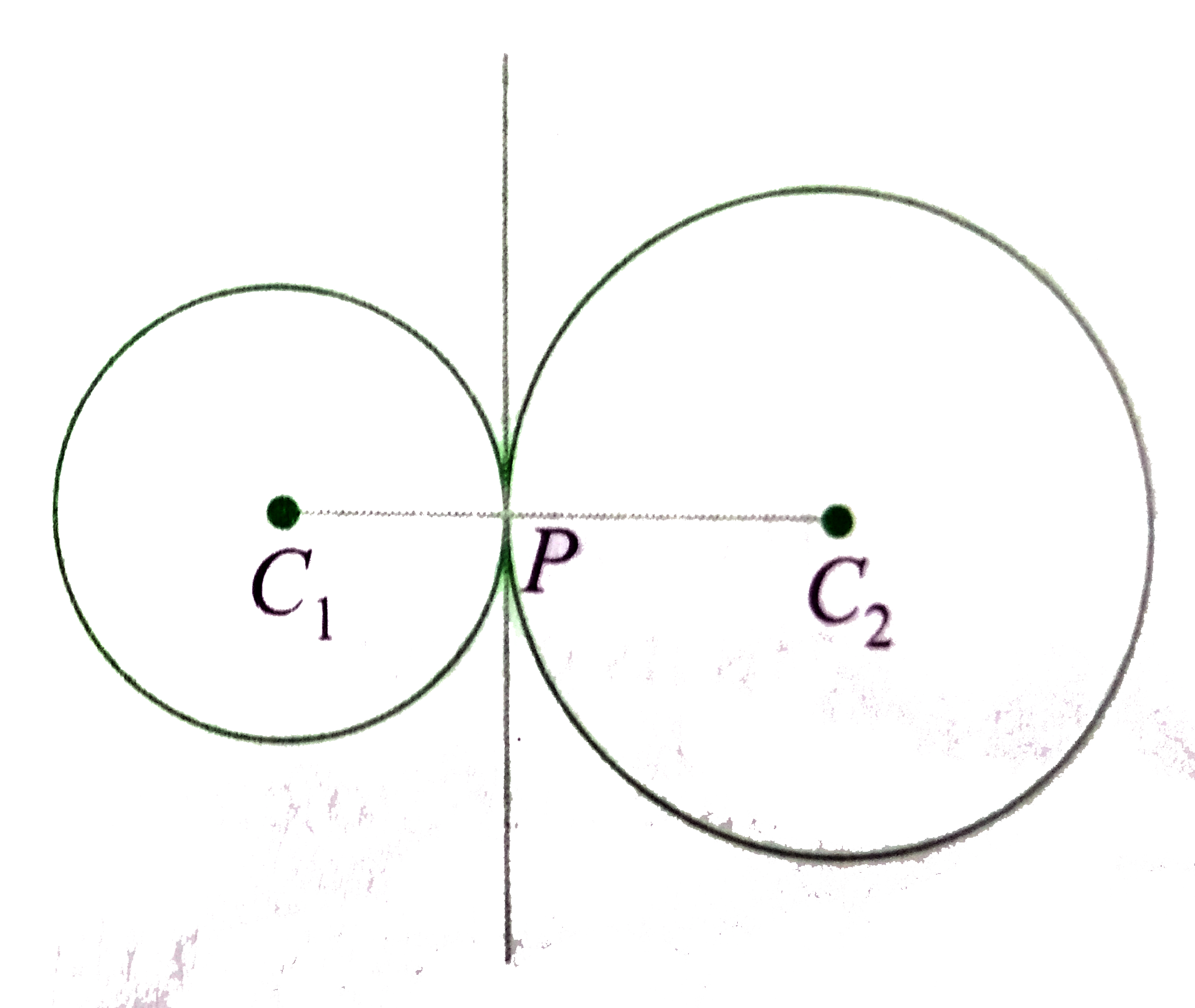
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
If the line xcosθ+ysinθ=2 is the equation of a transverse common tangent to the circles x2+y2=4 and x2+y2−6√3x−6y+20=0 , then the value of θ is 5π6 (b) 2π3 (c) π3 (d) π6
View SolutionIf the equation of tangent to the circle x2+y2−2x+6y−6=0 and parallel to 3x−4y+7=0 is 3x−4y+k=0 then the values of k are
View Solutioncot−1(−√3)=
(a) −π6 (b)5π6 (c)π3 (d)2π3
View SolutionThe line tangent to the curves y3−x2y+5y−2x=0 and x2−x3y2+5x+2y=0 at the origin intersect at an angle θ equal to π6 (b) π4 (c) π3 (d) π2
View SolutionThe angles at which the circles (x−1)2+y2=10andx2+(y−2)2=5 intersect is π6 (b) π4 (c) π3 (d) π2
View SolutionIf tanθ+secθ=√3, 0<θ<π, then θ is equal to 5π6 b. 2π3 c. π6 d. π3
View SolutionFrom the point P(2+3√2cosθ,3+3√2sinθ),0<θ<2π , tangents are draw to the circle x2+y2−4x−6y+4=0, then the angle between then is
View SolutionFor f(x)=sin2x,x∈(0,π) point of inflection is: π6 (b) 2π4 (c) 3π4 (d) 4π3
View SolutionIf the tangent at the point P(θ) to the ellipse 16x2+11y2=256 is also a tangent to the circle x2+y2−2x=15, then θ= 2π3 (b) 4π3 (c) 5π3 (d) π3
View SolutionThe angle subtended by common tangents of two ellipses 4(x−4)2+25y2=100and4(x+1)2+y2 at the origin is π3 (b) π4 (c) π6 (d) π2
View Solution
