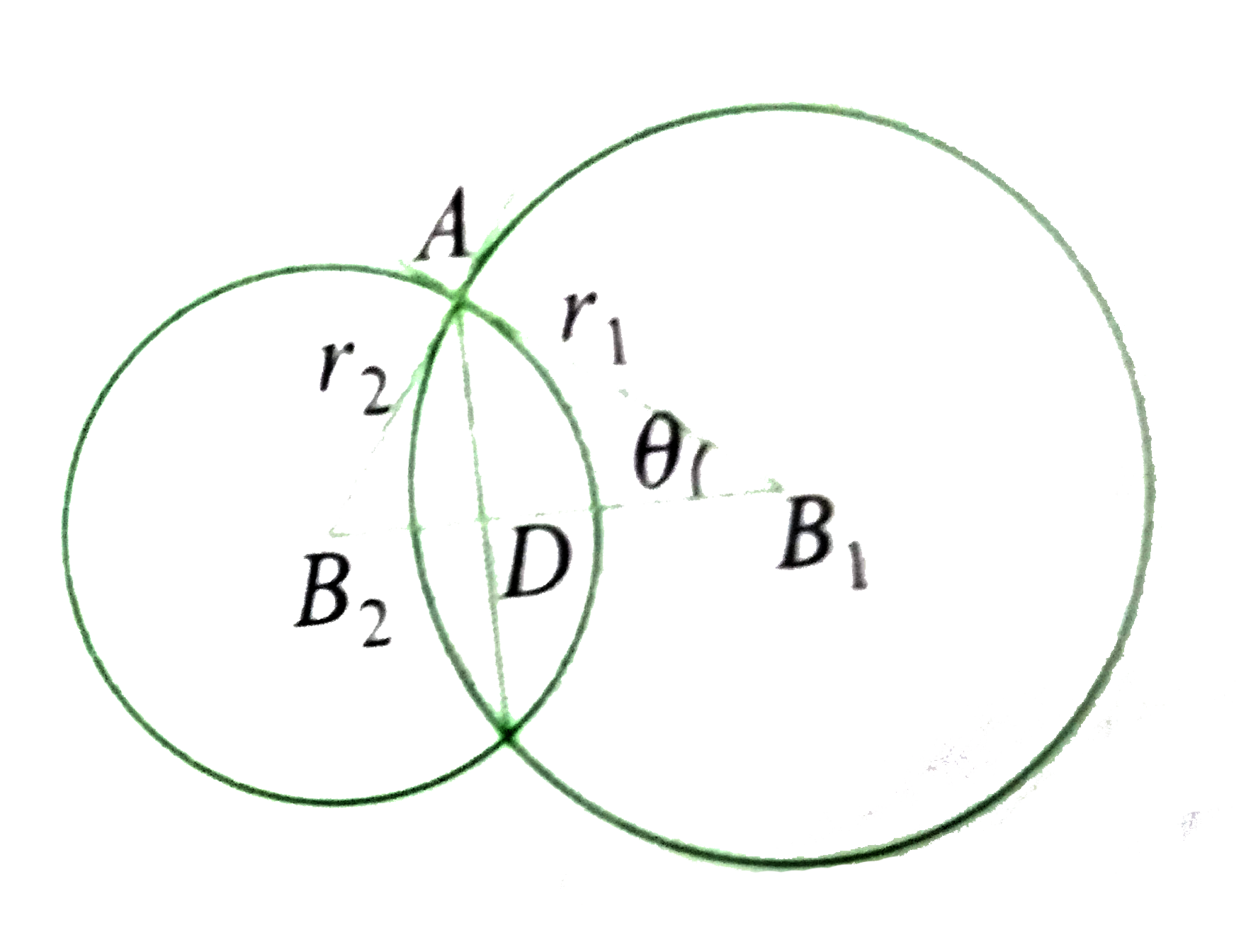
The circles having radii $r_{1} a n d r_{2}$ intersect orthogonally. The length of their common chord is $\frac{2 r_{1} r_{2}}{\sqrt{r 12 + r 12}}$ (b) $\frac{\sqrt{r 12 + r 12}}{2 r_{1} r_{2}}$ $\frac{r_{1} r_{2}}{\sqrt{r 12 + r 12}}$ (d) $\frac{\sqrt{r 12 + r 12}}{r_{1} r_{2}}$

A

$\frac{2 r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$

B

$\frac{\sqrt{r_{2}^{2} + r_{1}^{2}}}{2 r_{1} r_{2}}$

C

$\frac{r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$

D

$\frac{\sqrt{r_{2}^{2} + r_{1}^{2}}}{r_{1} r_{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

Let $∠ A B_{1} B_{2} = θ$ Then,
$A D = r_{1} sin θ$ ( In $Δ A D B_{1})$
and $A D = r_{2} cos θ (ln Δ A D B_{2})$
$∴ A D^{2} (\frac{1}{r_{1}^{2}} + \frac{1}{r_{2}^{2}}) = 1$
or $A D = \frac{r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$
Thus, length of common chord $= \frac{2 r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{1}^{2}}}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The circles having radii $r_{1} a n d r_{2}$ intersect orthogonally. The length of their common chord is $\frac{2 r_{1} r_{2}}{\sqrt{r 12 + r 12}}$ (b) $\frac{\sqrt{r 12 + r 12}}{2 r_{1} r_{2}}$ $\frac{r_{1} r_{2}}{\sqrt{r 12 + r 12}}$ (d) $\frac{\sqrt{r 12 + r 12}}{r_{1} r_{2}}$
A $\frac{2 r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$
B $\frac{r_{1} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$
C $\frac{2 r_{1}^{2} r_{2}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$
D $\frac{2 r_{2}^{2} r_{1}}{\sqrt{r_{1}^{2} + r_{2}^{2}}}$
Question 2 - Select One
$(r_{1} + r_{2}) (r_{2} + r_{3}) (r_{3} + r_{1}) =$
A $R s^{2}$
B $2 R s^{2}$
C $3 R s^{2}$
D $4 R s^{2}$
Question 3 - Select One
$(\frac{1}{r_{1}} + \frac{1}{r_{2}}) (\frac{1}{r_{2}} + \frac{1}{r_{3}}) (\frac{1}{r_{3}} + \frac{1}{r_{1}}) =$
A $\frac{16 R}{a b c}$
B $\frac{R^{3}}{4 a b c}$
C $\frac{64 R^{3}}{a^{2} b^{2} c^{2}}$
D $\frac{R^{3}}{a b c}$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile