Two circles which pass through the points A(0,a),B(0,−a) and touch the line y=mx+c wil cut orthogonally if
a2=c2(2m+1)
a2=c2(2+m2)
c2=a2(2+m2)
c2=a2(2m+1)
The correct Answer is:3
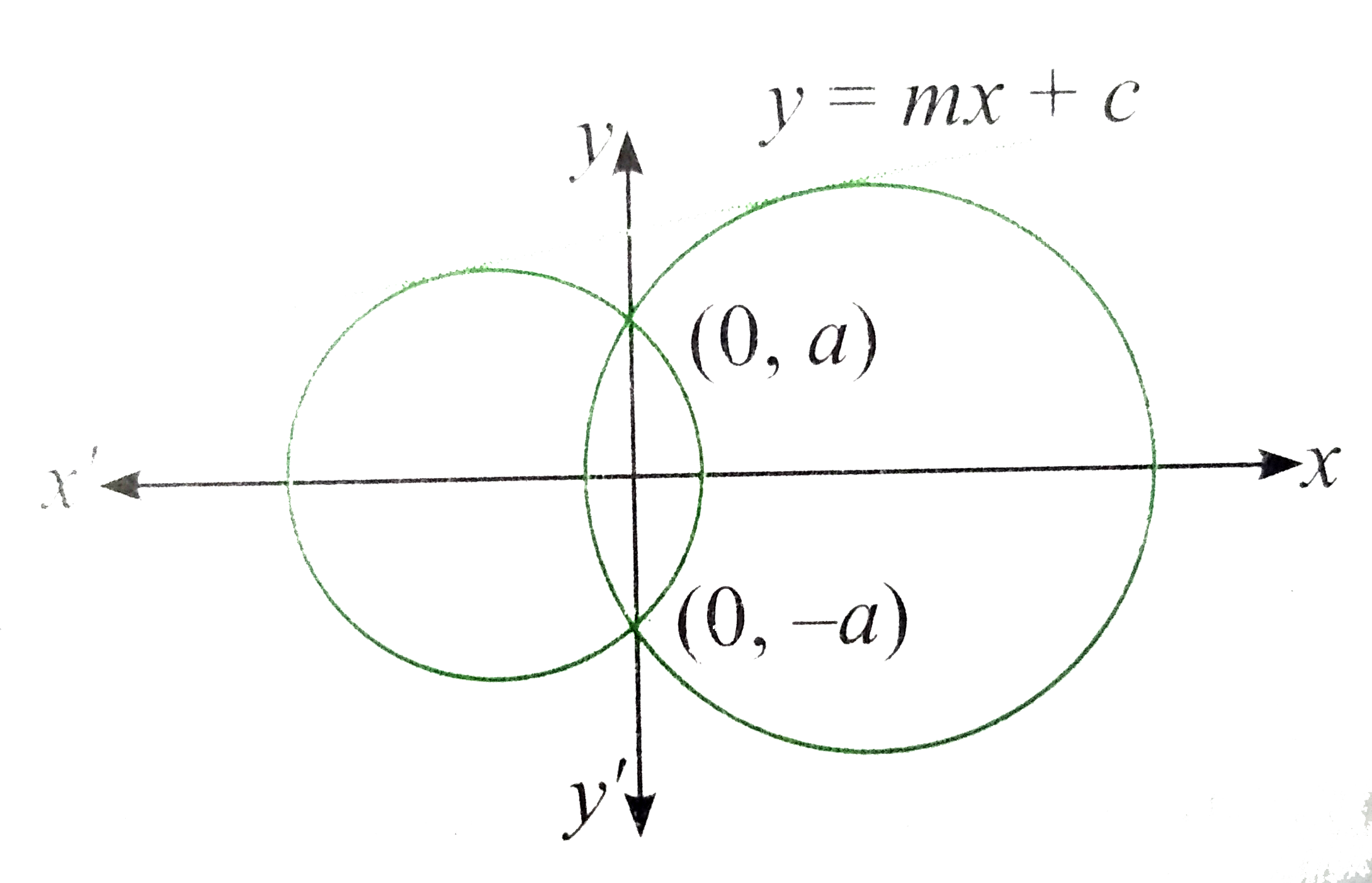
The equatio of the family of circles through (0,a) and (0,-a) is
[x2+(y−a)(y+a)]+λx=0,λ∈R
or x2+y2+λx−a2=0
Since circles touch line y=mx+c,
√(λ2)2+a2=|(−mλ/2)+c|√1+m2
or (1+m2)[λ24+a2]=(mλ2−c)2
or (1+m2)[λ24+a2]=m2λ24−mcλ+c2
or λ2+4mcλ+4a2(1+m2)−4c2=0
∴λ1λ2=4[a(1+m2)−c2]
or g1g2=[a2(1+m2)−c2]
Now, g1g2=f1f2=c1+c22 (As circle cut orthogonally.)
∴a2(1+m2)−c2=−a2
Hence, c2=a2(2+m2)
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
Prove that the two circles each of which passes through the point (0,k)and(0,−k) and touches the line y=mx+b will cut orthogonally, if b2=k2(2+m2).
View SolutionP(a, b) is a point in first quadrant. If two circles which passes through point P and touches both the coordinate axis, intersect each other orthogonally, then
View Solution
Knowledge Check
A variable circle is described to pass through the point (a, 0) and touch the line x+y=0. Locus of the centre of the above circle is
AparabolaBellipseChyperbolaDnone of theseThe locus of the centere of a circle which passes through the point (0,0) and cuts off a length 2b from the line x=c is-
Ay2+2cx=b2+c2Bx2+cx=b2+c2Cy2+2cy=b2+c2Dnone of theseThe centre of a circle passing through the points (0, 0), (1, 0) and touching the circle x2+y2=9, is
A(32,12)B(12,32)C(12,12)D(12,−21/2)
The centre of a circle passing through the points (0, 0), (1, 0) and touching the circle x2+y2=9, is
View SolutionThe centre of a circle passing through the points (0, 0), (1, 0) and touching the circle x2+y2=9, is
View SolutionFind the equation of the circle passing through the point (1,9), and touching the line 3x+4y+6=0 at the point (-2,0) .
View SolutionA circle passes through the points (0,0) and (0, 1) and also touches the circie x2+y2=16 The radius of the circle is
View SolutionThe radius of the least circle passing through the point (8,4) and cutting the circle x2+y2=40 orthogonally is
View Solution
