If the length of the common chord of two circles x2+y2+8x+1=0 and x2+y2+2μy−1=0 is 2√6 , then the values of μ are ±2 (b) ±3 (c) ±4 (d) none of these
A
±2
B
±3
C
±4
D
none of these
Video Solution
Text Solution
The correct Answer is:2
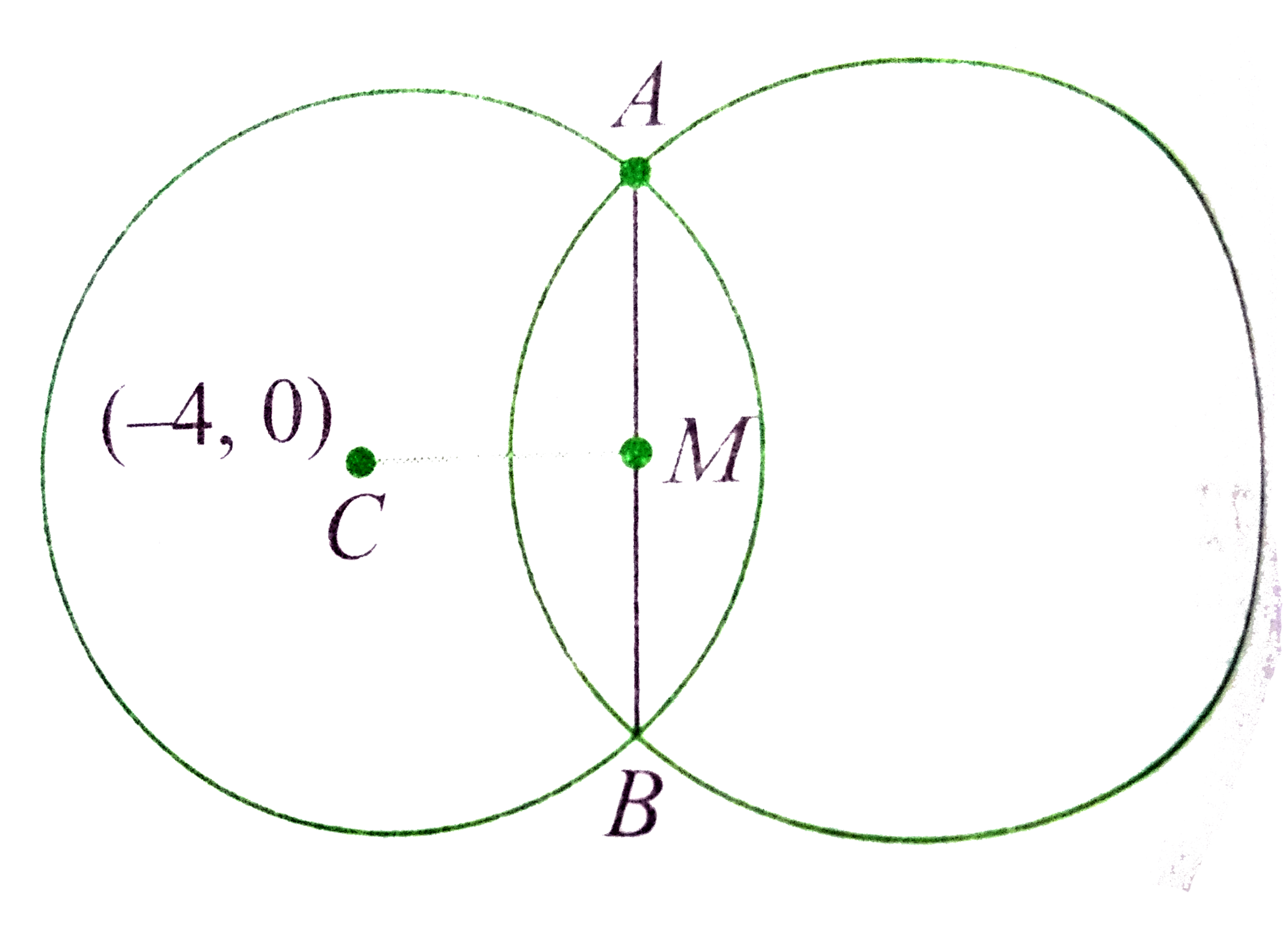
The common choard is S1−S2=0
4x−μy+1=0
∴AC= Radius of first circle =√15
AM=AB2=√6
∴CM=3
∴|−16+1|√16+μ2=3
or μ=±3
|
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
Knowledge Check
The length of the common chord of the two circle x2+y2−4y=0 and x2+y2−8x−4y+11=0 is
A√1454 cmB√112 cmC√135 cmD√1354 cmThe length of the common chord of the circles x2+y2+2x+3y+1=0 and x2+y2+4x+3y+2=0 is
A92B2√2C3√2D32The length of the common chord of the circles x2+y2−2x−1=0 and x2+y2+4y−1=0, is
A√15/2B√15C2√15Dnone of these
The length of the common chord of the two circles x2+y2−4y=0 and x2+y2−8x−4y+11=0 is
View SolutionFind the length of the common chord of the circles x2+y2+2x+6y=0 and x2+y2−4x−2y−6=0
View SolutionThe lengths of the common tangents of the circles x2+y2+4x=0andx2+y2−6x=0 is
View SolutionThe length of the common chord of the circles x2+y2−2x+4y−20=0,x2+y2+6x+10y−2=0 is
View SolutionIf 2x−3y=0 is the equation of the common chord of the circles, x2+y2+4x=0 and x2+y2+2λy=0, then the value of λ is
View Solution
