From an arbitrary point P on the circle x2+y2=9 , tangents are drawn to the circle x2+y2=1 , which meet x2+y2=9 at AandB . The locus of the point of intersection of tangents at AandB to the circle x2+y2=9 is x2+y2=(277)2 (b) x2−y2(277)2 y2−x2=(277)2 (d) none of these

A

x2+y2=(27/7)2

B

x2−y2=(27/7)2

C

y2−x2=(27/7)2

D

none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:1

Since ΔPOQ and ΔAOQ are congruent,
∠POQ=∠QOA=θ
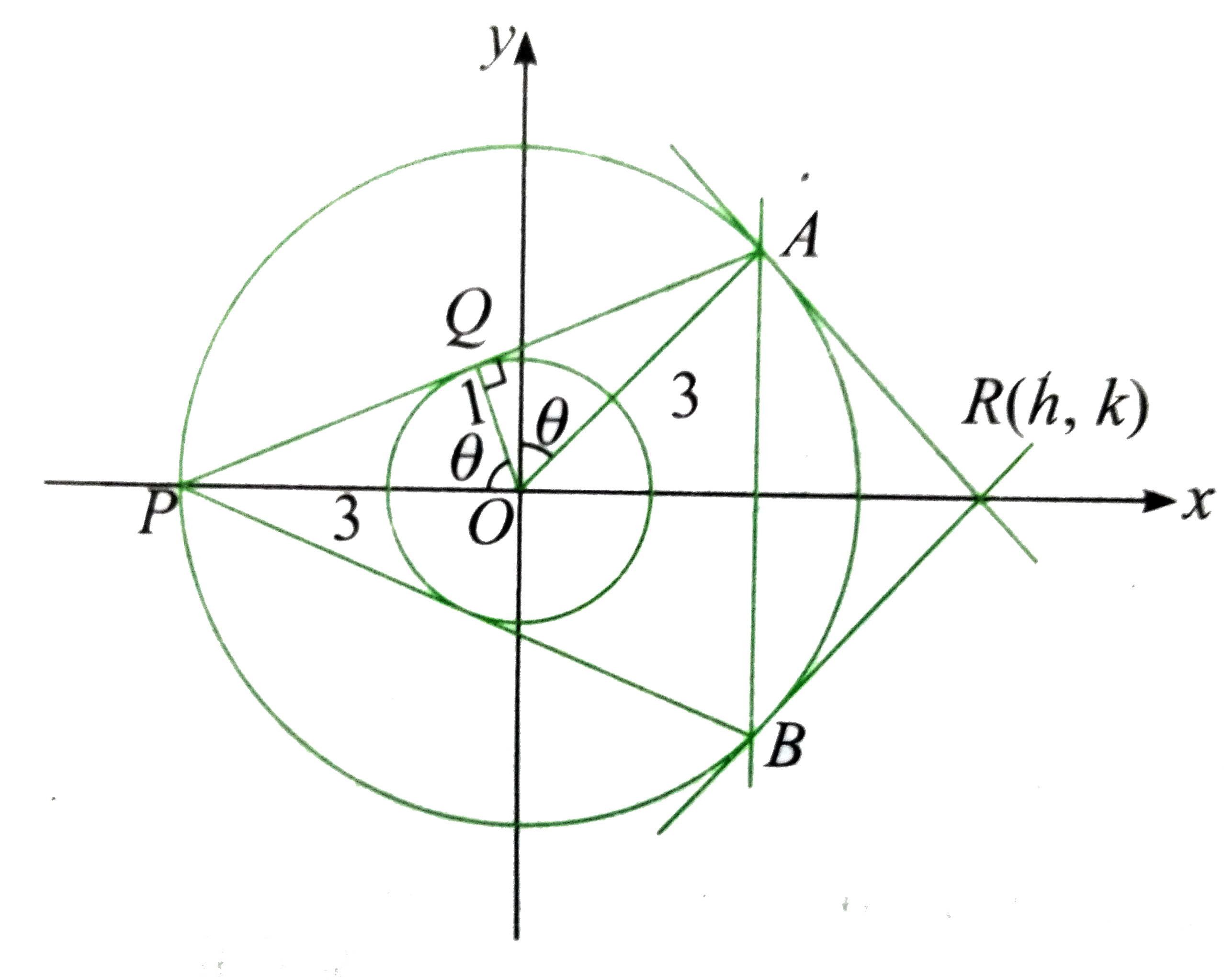
ocr_image
cosθ=12, since ∠POR=π
∴∠AOR=π−2θ
Now, in triangle AOR,∠AOR=π−2θ and AO=3 units
Therefore,
cos(π−2θ)=OAOR=3√h2+k2
or √h2+k2=277
or x2+y2=(277)2

Updated on:21/07/2023
|
Class 12MATHSCIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The locus of the point of intersection of perpendicular tangents to the circles x2+y2=a2 and x2+y2=b2 , is

    Ax2+y2=a2−b2
    Bx2+y2=a2+b2
    Cx2+y2=(a+b)2
    Dnone of these

  • If the tangents are drawn to the circle x2+y2=12 at the point where it meets the circle x2+y2−5x+3y−2=0, then the point of intersection of these tangents is

    A(6, -6)
    B(6,18/5)
    C(6,−18/5)
    Dnone of these