The equation of the locus of the middle point of a chord of the circle x2+y2=2(x+y) such that the pair of lines joining the origin to the point of intersection of the chord and the circle are equally inclined to the x-axis is x+y=2 (b) x−y=2 2x−y=1 (d) none of these
x+y=2
x−y=2
2x−y=1
none of these
The correct Answer is:1
Solving y=mx and x2+y2−2x−2y=0, we get
x2+m2x2−2x−2mx=0
or x=0,2(1+m)1+m2
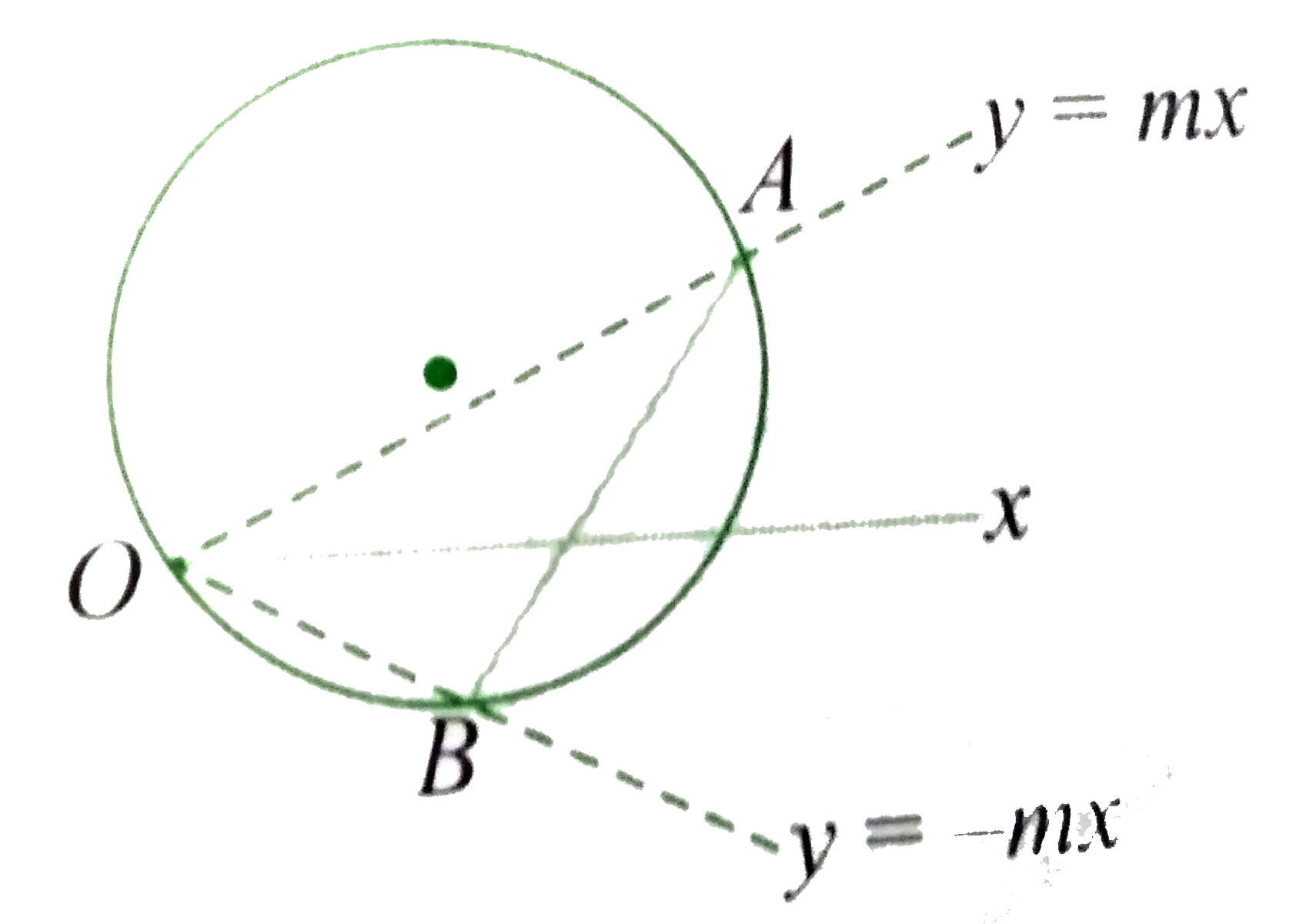
Similarly, solving y=−mx and the equation of the circle , we get
x=0,2(1−m)1+m2
:>A≡(2(1+m)1+m2,2m(1+m)1+m2)
and B≡(2(1−m)1+m2,−2m(1−m)1+m2)
Let the middle point of AB be (α,β). Then
α=12{2(1+m)1+m2,−2(1−m)1+m2}
and β=12{2m(1+m)1+m2,−2(1−m)1+m2}
∴α=21+m2,β=2m21+m2
Eliminating m from these, we get α+β=2.
Hence, the locus is x+y=2.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
Find the locus of the mid point of all chords of the circle x2+y2−2x−2y=0 such that the pairof . lines joining (0, 0) & the point of intersection of the chords with the circles make equal an axis of x.
View SolutionThe equation of pair of lines joining origin to the points of intersection of x2+y2=9 and x+y=3
View Solution
Knowledge Check
The equation of pair of lines joining origin to the points of intersection of x2+y2=9 and x+y=3 is :
Ax2+(3−x)2=9Bxy=0C(3+y)2+y2=9D(x−y)2=9The equation of pair of lines joining origin to the points of intersection of x2+y2=9 and x+y=3 is :
Ax2+(3−x)2=9Bxy=0C(3+y)2+y2=9D(x−y)2=9The locus of the middle points of chords of the circle x2+y2=25 which are parallel to the line x−2y+3=0, is
Ax+2y=0B2x+y=0Cx-2y=0D2x-y=0
The equation to the pair of lines joining the origin to the points of intersection of y=x+3 and 2x2+2y2=1 is
View SolutionThe locus of the middle points of the focal chords of the parabola, y2=4x is:
View SolutionFind the locus of the middle points of the chords of the circle x2+y2=a2which pass through a given point(x1,y1)
View SolutionFind the equation of line joining origin to the point of intersection of the pair of lines 3x+y=10 and x−y=2.
View SolutionThe equation of the straight line joining the origin to the point of intersection of y-x+7=0 and y+2x-2=0 is
View Solution
