Question

The circle $x^2+y^2=4$cuts the line joining the points $A(1,0)$ and $B(3,4)$ in two points $P$ and $Q$. Let $B\frac{P}{P}A=\alpha$ and $B\frac{Q}{Q}A=\beta$. Then $\alpha$ and $\beta$ are roots of the quadratic equation

Options

A. `3x^(2)-16x+21=0`
B. `x^(2)-8x+7=0`
C. `x^(2)-9x+8=0`
D. none of these

Answer

1

Explanation

The equation of the line joining A(1,0) and B(3,4) is `y=2x-2`
This cuts the circle `x^(2)+y^(2)=4` at `Q(0,-2)` and `P(8//5,6//5)`. We have `BQ =3sqrt(5),QA=sqrt(5), BP =7 sqrt(5) ` and `PA =3sqrt(5)` . Therefore,
`alpha=(BP)/(PA)=(7sqrt(5))/(3sqrt(5))=(7)/(3)`
and `beta=( BQ)/(QA)=(3sqrt(5))/(sqrt(5))=3`

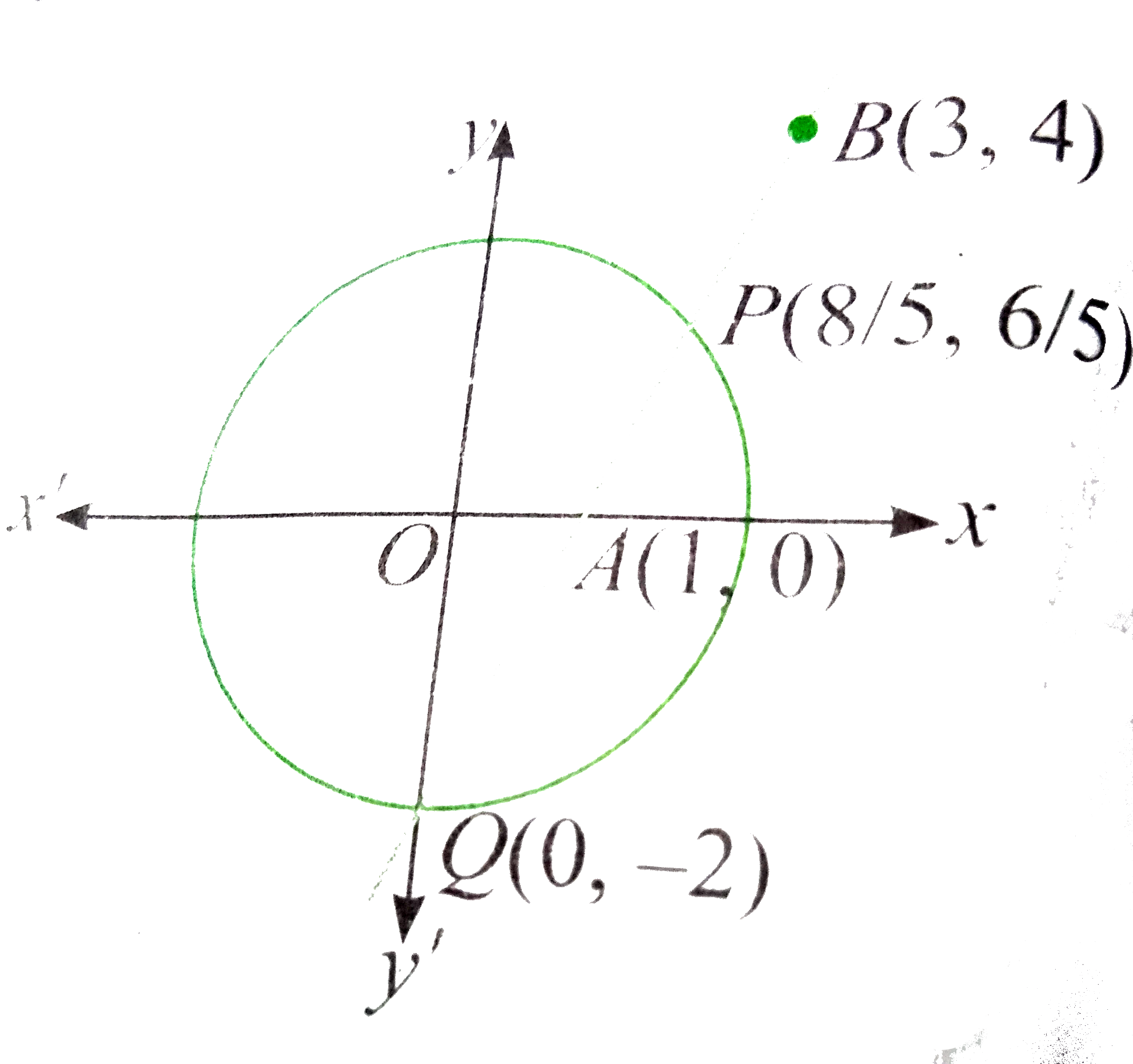
Therefore, `alpha` and `beta` are roots of the equation
`x^(2)-x(alph+beta)+alphabeta=0`
i.e., `x^(2)-x((7)/(3)-3)+(7)/(3)(3)=0`
or `3x^(2)-16x+21=0`