A region in the $x - y$ plane is bounded by the curve $y = \sqrt{25 - x^{2}}$ and the line $y = 0$ . If the point $(a, a + 1)$ lies in the interior of the region, then

A

$a \in (- 4, 3)$

B

$a \in (- \infty, - 1) \in (3, \infty)$

C

$a \in (- 1), 3)$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

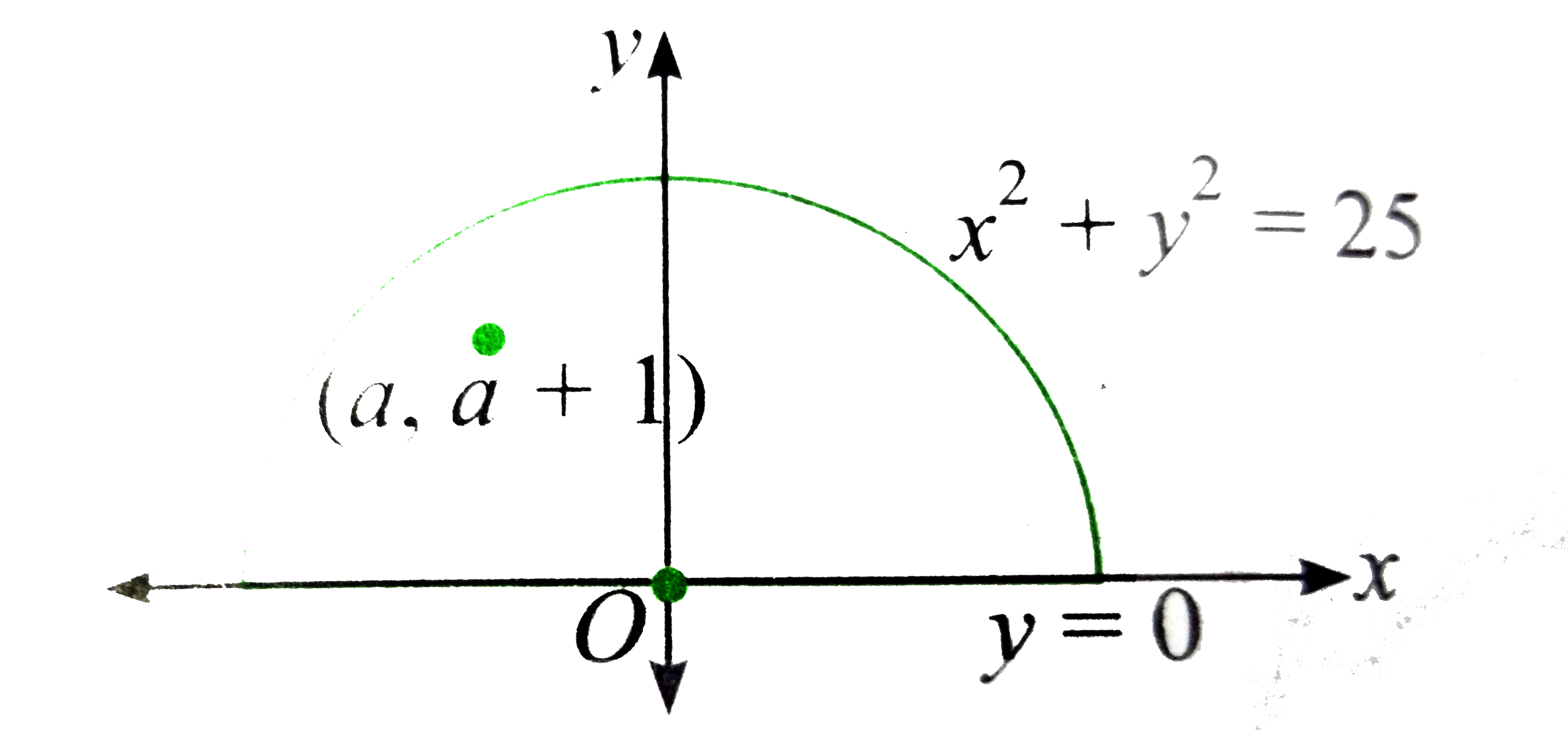
$y = \sqrt{25 - x^{2}}$ and $y = 0$ bound the semicircle above the x-axis .
Therefore,
$a + 1 > 0$ (1)
and $a^{2} + {(a + 1)}^{2} - 25 < 0$ or $2 a^{2} + 2 a - 24 < 0$
or $a^{2} + a - 12 < 0$
or $- 4 < a < 3$ (2)
From (1) and (2),
$- 1 < a < 3$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area of the region bouned by the curve $y = 2 x - x^{2}$ and the line $y = x$ is
A $1 / 2$
B $1 / 3$
C $1 / 4$
D $1 / 6$
The area of the region bounded by the curve $y = x^{2}$ and the line $y = 16$ is :
A $\frac{32}{3}$
B $\frac{256}{3}$
C $\frac{64}{3}$
D $\frac{128}{3}$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile