Find the are of the region bounded by the curve y=x2+2 and the lines y=x,x=0and3
Video Solution
Text Solution
y=x2+2⇒x2=(y−2)
Clearly , x2=(y−2) represents an upward parabola with its vertex at A (0,2)
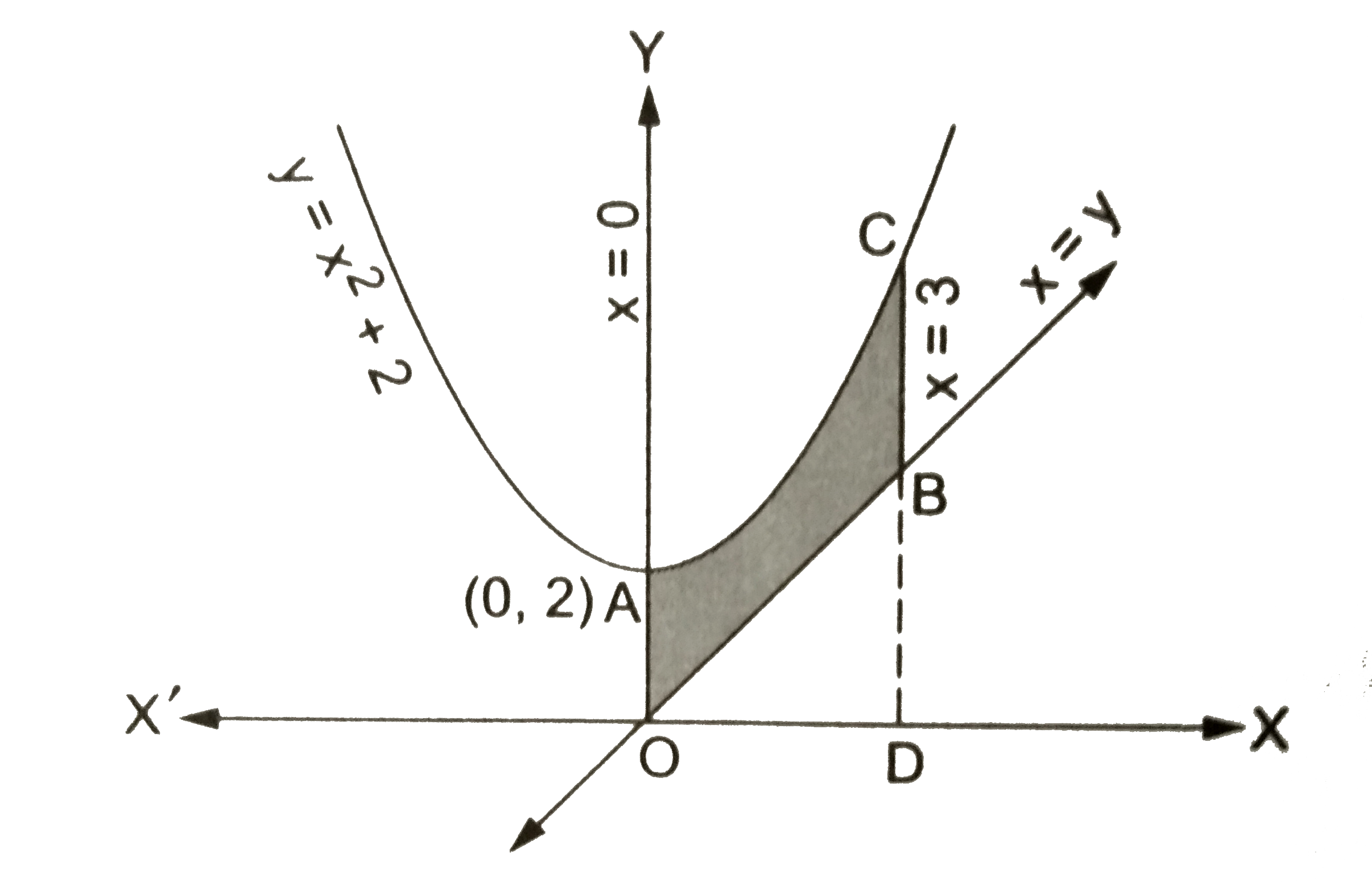
Also , y = x represents the straight line , making an angle of 45∘ with the positive direction of the x-axis .
And x = 0 is the y-axis , while x = 3 represents a ling parallel to the y-axis at a distance of 3 units from it .
Thus , the shaded region in the given figure is the required area .
∴ required area = (area ODCAO) - (area ODBO)
=3∫0(x2+2)dx−3∫0xdx
= [x33+2x]30−[x22]30=(15−92)=212 sq units .
Hence , the required area is 212 sq units .
|
Topper's Solved these Questions
- AREA OF BOUNDED REGIONS BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 17
39 Videos
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions
89 Videos
- BAYES'S THEOREM AND ITS APPLICATIONSBOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 30
18 Videos
Similar Questions
Knowledge Check
The area of the region bouned by the curve y=2x−x2 and the line y=x is
A1/2B1/3C1/4D1/6The area of the region bounded by the curve y=x2 and the line y=16 is :
A323B2563C643D1283
Find the area of the region bounded by the curve y=x2 and the line y=4.
View SolutionFind the area of the region bounded by the curve y2=4x and the line x=3.
View SolutionFind the area of the region bounded by the curves y=x3 and the lines y=x+6 and y=0.
View SolutionThe area of the region bounded by the curve y=2x−x2 and the line y=x is
View SolutionFind the area of the region bounded by the curve xy=1 and the lines y=x,y=0,x=e
View SolutionFind the area of the region bounded by the curve y-3 and the lines y = x + 6 and y =0.
View Solution
