A circle of constant radius a passes through the origin O and cuts the axes of coordinates at points P and Q . Then the equation of the locus of the foot of perpendicular from O to PQ is (x2+y2)(1x2+1y2)=4a2 (x2+y2)2(1x2+1y2)=a2 (x2+y2)2(1x2+1y2)=4a2 (x2+y2)(1x2+1y2)=a2
(x2+y2)(1x2+1y2)=4a2
(x2+y2)2(1x2+1y2)=a2
(x2+y2)2(1x2+1y2)=4a2
(x2+y2)(1x2+1y2)=a2
The correct Answer is:3
The equation of line PQ is
y−k=−hk(x−h)
or hx+ky=h2+k2
∴Q=(h2+k2h,0)
and P≡(0,h2+k2k)
Also, 2a=√x21+y21
or x21+y21=4a2
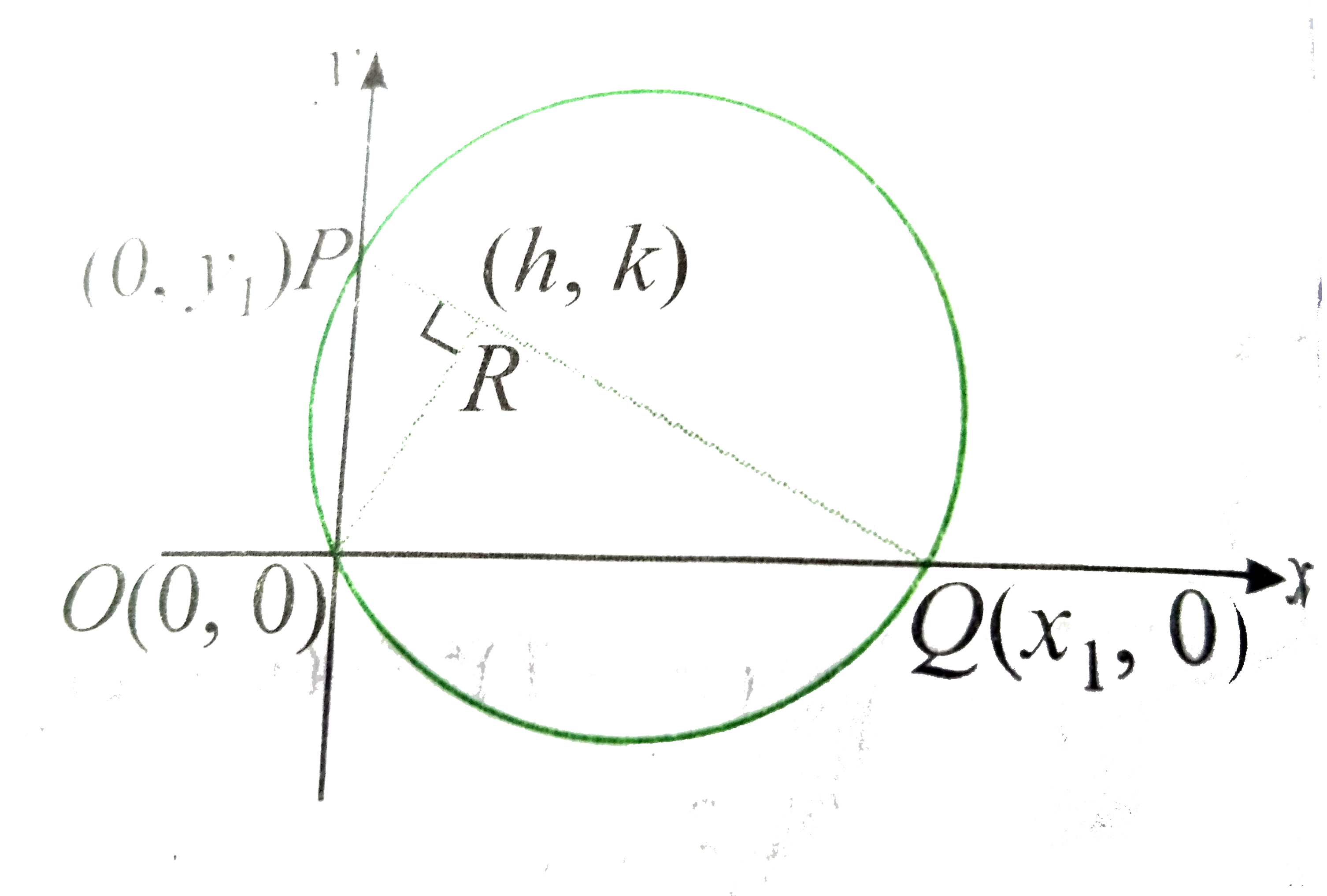
Eliminating x1 and y1, we have
(x2+y2)(1x2+1y2)=4a2
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
A circle of radius r passes through origin and cut the y-axis at P and Q. The locus of foot of perpendicular drawn from origin upon line joining the points P and Q is (A) (x2+y2)3=r2(x2y2) (B) (x2+y2)2(x+y)=r2(xy) (C) (x2+y2)2=r2(x2y2) (D) (x2+y2)3=4r2(x2y2)
View SolutionThe locus of the foot of perpendicular drawn from the centre of the ellipse x2+3y2=6 on any tangent to it is (1) (x2−y2)2=6x2+2y2 (2) (x2−y2)2=6x2−2y2 (3) (x2+y2)2=6x2+2y2 (4) (x2+y2)2=6x2−2y2
View Solution
Knowledge Check
If x2+y2+1x2+1y2=4 then the value of x2+y2 is
A2B4C8D16If x=a12+a−12,y=a12−a−12 then value of (x4−x2y2−1)+(y4−x2y2+1).
A16B13C12D14
The equation of the curve passing through origin, whose slope at any point is x(1+y)1+x2, is (A) (1+y)2−x2=1 (B) x2+(y+1)2=1 (C) (x+y)y=1−x2 (D) x=ye(1+y)
View SolutionLet P be the point (1, 0) and Q be a point on the locus y2=8x . The locus of the midpoint of PQ is y2+4x+2=0 y2−4x+2=0 x2−4y+2=0 x2+4y+2=0
View SolutionFind the equation of line joining the center of the circles x2+y2−2x+4y+1=0 and 2x2+2y2−2y+4x+1=0
View SolutionAdd:
x2y2−1,y2−1−x2,1−x2−y2
View SolutionShow that the equation of the chord of the parabola y2=4ax through the points (x1,y1)and(x2,y2) on it is : (y−y1)(y−y2)=y2−4ax
View SolutionProperty 4: The equation of the family of circles passing through two given points P(x1,y1)andQ(x2,y2)
View Solution
