For any real t,x=12(et+e−t),y=12(et−e−t) is a point on the hyperbola x2−y2=1 Show that the area bounded by the hyperbola and the lines joining its centre to the points corresponding to t1and−t1 ist1.
The correct Answer is:e2t1−e−2t14−14(e2t1−e−2t1−4t1)
Let P=(et1+e−t12,et1−e−t12)
andQ=(e−t+et12,e−t1−et2)
We have to find the area of the region bounded by the curve x2−y2=1 and the lines joining the centre x=0,y=0 to the points (t1)and(−t1).
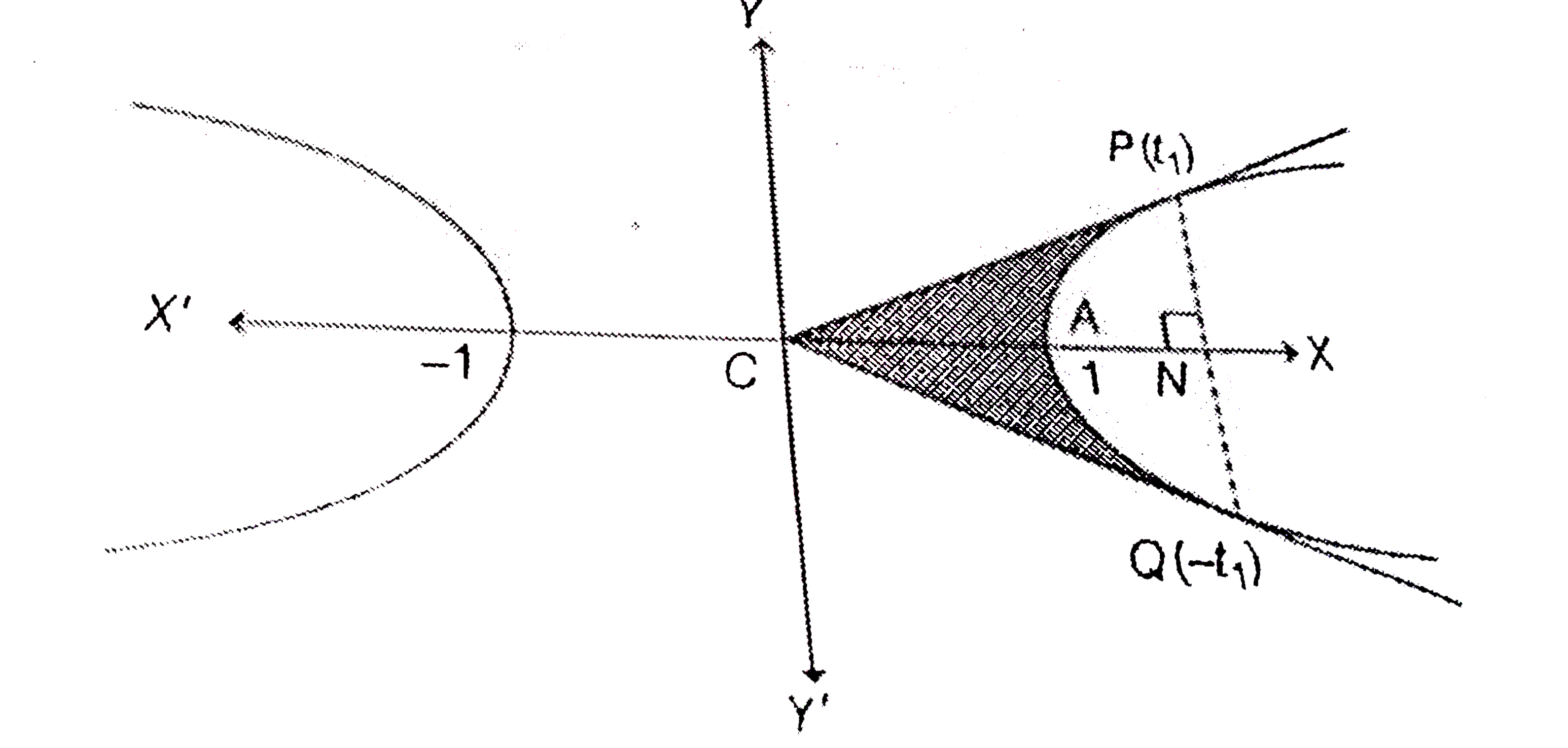
=2⎡⎢⎣area of ΔPCN−∫et1+e−t121ydx⎤⎥⎦
=2[12(et1+e−t12)(et1−e−t12)−∫t11ydydx⋅dt]
=2[e2t1−e−2t18−∫t10(et−e−t2)dt]
=e2t1−e−2t14−12∫t10(e2t+e−2t−2)dt
=e2t1−e−2t14−12[e2t2−e−2t2−2t]
=e2t1−e−2t14−14(e2t1−e−2t1−4t1)
Topper's Solved these Questions
- AREABook:IIT JEE PREVIOUS YEARChapter:AREAExercise:AREA USING INTEGRATION
Explore 55 Videos
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)
Explore 8 Videos
- BINOMIAL THEOREMBook:IIT JEE PREVIOUS YEARChapter:BINOMIAL THEOREMExercise:Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
Explore 8 Videos
Similar Questions
For any real t,x=12(et+e−t),y=12(et−e−t) is a point on the hyperbola x2−y2=1 Show that the area bounded by the hyperbola and the lines joining its centre to the points corresponding to t1and−t1 ist1.
View SolutionShow that the area formed by the normals to y2=4ax at the points t1,t2,t3 is
View Solution
Knowledge Check
x=et+e−t2,y=et−e−t2,t∈R represents
AAn ellipseBA prabolaCA hyperbolaDA circleIf x=et+e−t2,y=et−e−t2, then: dydx=
AxyByxC−xyD−yxThe equation x=et+e−t2,y=et−e−t2,t∈R, represents
AAn ellipseBA parabolaCA hyperbolaDA circel
Find the area of the region bounded by the curve x=at2 and y=2at between the ordinates corresponding to t = 1 and t = 2.
View SolutionFind the area bounded by x=at2andy=2at between the ordinates corresponding to t=1andt=2.
View SolutionShow that the tangents and the normals to the parabola x=at2, y=2at at points corresponding to t = 1 and t = -1 form a square.
View SolutionThe locus of point (et+e−t2,et−e−t2) is a hyperbola with eccentricity
View SolutionShow that the normal to the rectangular hyperbola xy=c2 at the point t meets the curve again at a point t' such that t3t'=−1.
View Solution