If the area (in sq. units) bounded by the parabola y2=4λx and the line y=λx,λ>0, is 19, then λ is equal to:
A
2√6
B
48
C
24
D
4√3
Video Solution
Text Solution
The correct Answer is:C
Given , equation of curves are
y2=4λx …(i)
andy=lalmbdax …(ii)
λ>0
Area bounded by above two curve is, as per figure
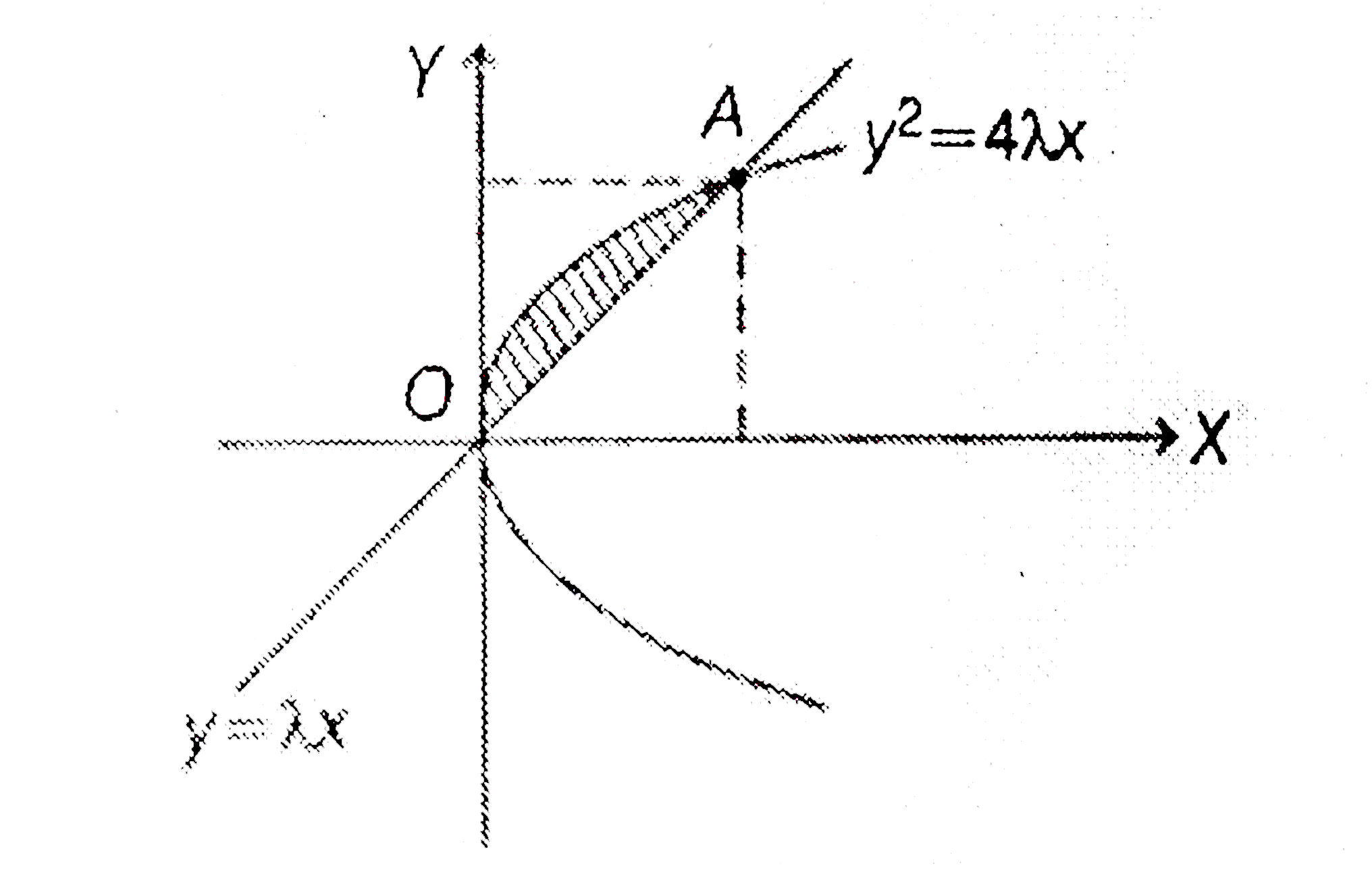
the intersection point A we will get on the solving Eqs. (i) and (ii) we get
λ2x2=4λx
⇒x=4λ, so y=4
So, A(4λ,4)
Now, required area is
=∫4/λ0(2√λx−λx)dx
=2√λ⎡⎣x3/232⎤⎦4/λ0−λ[x22]4/λ0
=43√λ4√4λ√λ−λ2(4λ)2
=323λ−8λ=32−243λ=83λ
It is given that area =19
⇒83λ=19
⇒λ=24
|
Topper's Solved these Questions
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)
Explore 8 Videos
- BINOMIAL THEOREMBook:IIT JEE PREVIOUS YEARChapter:BINOMIAL THEOREMExercise:Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
Explore 8 Videos
Similar Questions
Knowledge Check
If the area (in sq. units) bounded by the parabola y2=4λx and the line y=λx,λ>0, is 19, then λ is equal to:
A2√6B48C24D4√3if the area enclosed by the curves y2=4λx and y=λx is 19 square units then value of λ is
A24B37C48D38The area bounded by y=√1−x2 and y=x3−x is divided by y - axis in the ratio λ:1(∀λ>1), then λ is equal to
Aπ+1π−1Bππ−1Cπ+1πDπ+2π−2
If z=x+iy,z1/3=a−ibandxa−yb=λ(ay−by), then λ is equal to
View SolutionIf (x+y)2=2(x2+y2) and (x–y+λ)2=4,λ>0, then λ is equal to
View SolutionThe area of the region (in sq units), in the first quadrant, bounded by the parabola y=9x2 and the lines x = 0, y = 1 and y = 4, is
View SolutionIf the line y=2x+λ be a tangent to the hyperbola 36x2−25y2=3600, then λ is equal to
View SolutionThe angle between x2+y2−2x−2y+1=0 and line y=λx+1−λ, is
View Solution
