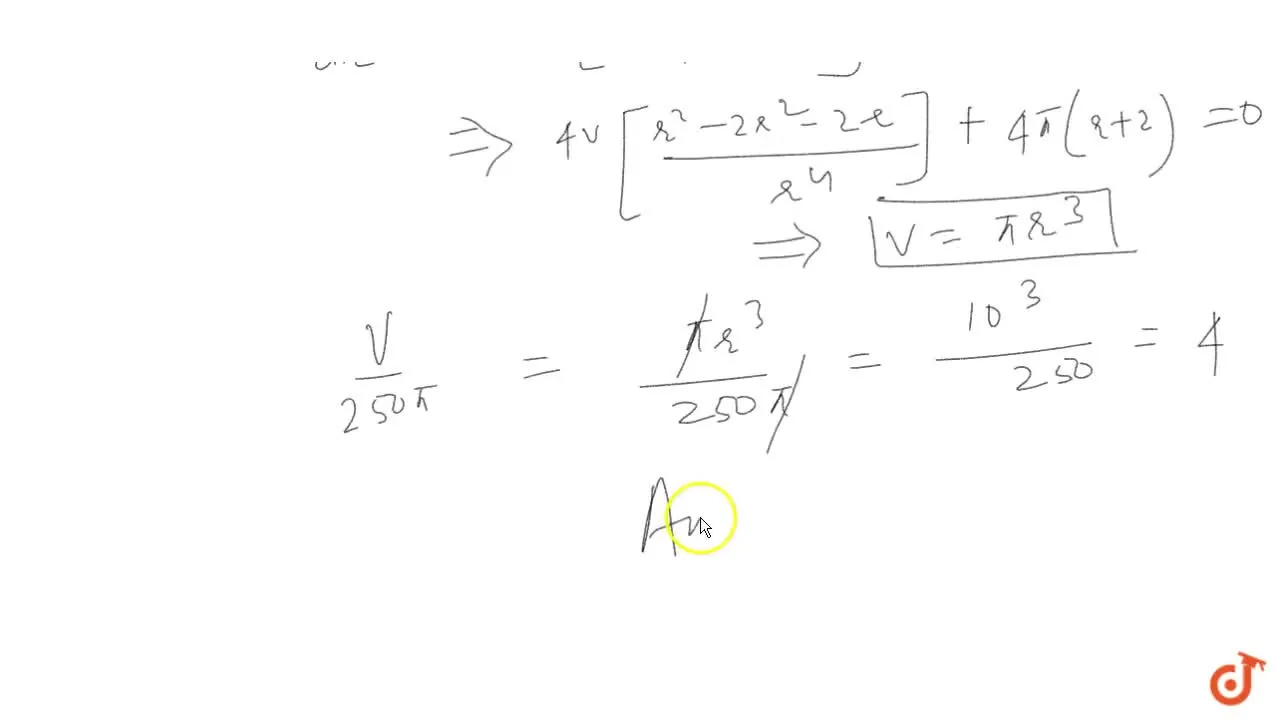A cylindrica container is to be made from certain solid material with the following constraints: It has a fixed inner volume of Vm3, has a 2 mm thick solid wall and is open at the top. The bottom of the container is a solid circular disc of thickness 2mm and is of radius equal to the outer radius of the container. If the volume the material used to make the container is minimum when the inner radius of the container is 10mm. then the value of V250π is
The correct Answer is:4
Here, volume of cylindrical container, V=πr2h … (i)
and let volume of the meterical used be T.
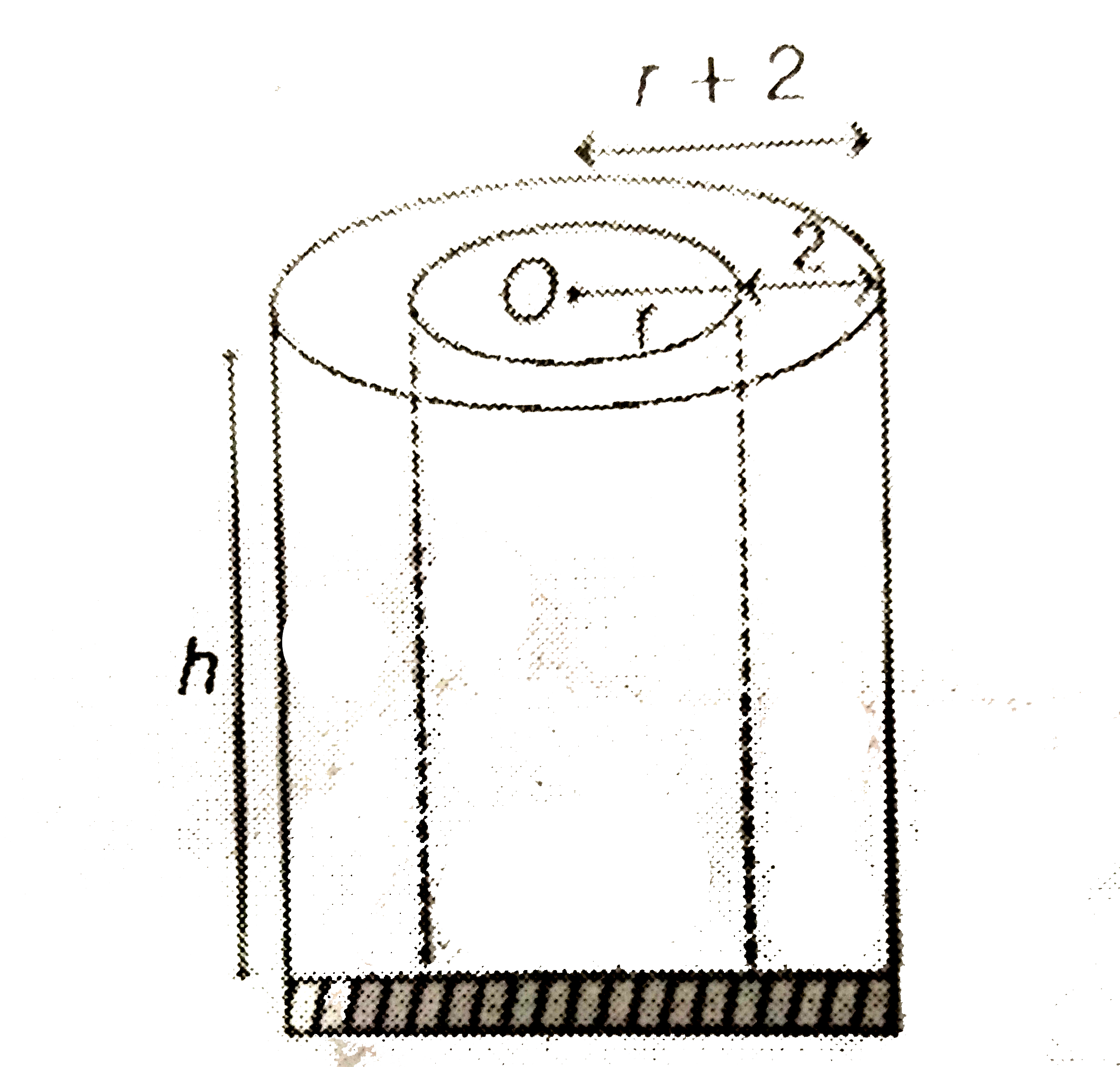
∴ T=π[(r+2)2−r2]h+π(r+2)2×2
⇒ T=π[(r+2)2−r2]⋅Vπr2+2π(r+2)2
[∵V=πr2h⇒h=Vπr2]
⇒T=V(r+2r)2+2π(r+2)2−V
On differentiating w.r.t. r, we get
dTdr=2V⋅(r+2r)⋅(−2r2)+4π(r+2)
At r=10,dTdr=0
Now, 0(r+2)⋅4(π−Vr3)
⇒ Vr3=π
where r=10
⇒ V1000=π
or V250π=4
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA (ANALYTICAL & DESCRIPTIVE QUESTIONS )20videos
APPLICATION OF DERIVATIVES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Integer Answer Type Question)1videos
3D Geometry
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - AREAEXERCISE - AREA USING INTEGRATION55videos
AREA
Similar Questions
A cylindrical container is to be made from certain solid material with the following constraints: It has a fixed inner volume of Vmm3, has a 2 mm thick solid wall and is open at the top. The bottom of the container is a solid circular disc of thickness 2 mm and is of radius equal to the outer radius of the container.
If the volume of the material used to make the container is minimum when the inner radius of the container is 10 mm, then the value of V250π isView SolutionThe outer radius of a spherical container is 5 cm and the thickness of the container is 2 cm . Find the volume of the metal content of the shell .
View SolutionA hollow hemispherical bowl of thickness 1 cm has an inner radius of 6 cm. Find the volume of metal required to make the bowl.
View SolutionThe outer radius of a spherical container is 5 cm and the thickness of the container is 2 cm.Find the volume of the metal content of the shell.
View SolutionA hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m,then find the volume of the iron used to make the tank
View SolutionWhat is the volume of the material in a spherical shell with inner radius ‘r' and outer radius 'R' ?
View SolutionThe material which is commonly used for making kitchen containers is
View SolutionA metallic sphere 1 dm in diameter is beaten into a circular sheet of uniform thickness equal to 1 mm. Find the radius of the sheet.
View SolutionIf a solid right circular cylinder is made of iron is heated to increae its radius and height by 1% each , then the volume of the solid is increased by :
View SolutionIf a solid right circular cylinder is made of iron is heated to increae its radius and height by 1% each , then the volume of the solid is increased by :
View Solution