The area (in sq. units) of the region bounded by the curves y=2x and y=|x+1|, in the first quadrant is :
A
32
B
loge2+32
C
12
D
32−1loge2
Video Solution
Text Solution
The correct Answer is:D
Given, equation of curves
y=2xandy=|x+1|={x+1 ,x≥−1−x−1 ,x<−1
∵ The figure of above given curves is
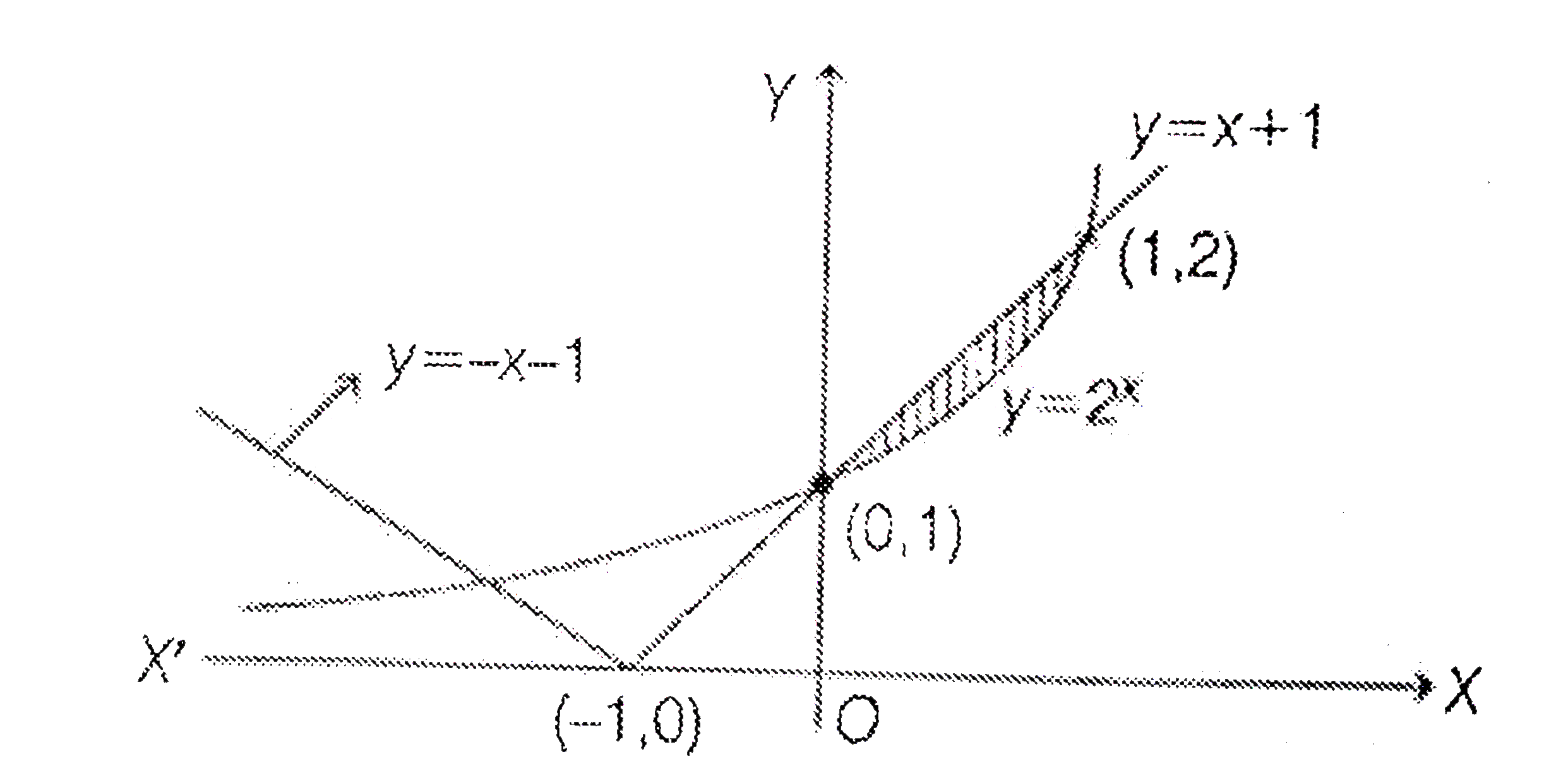
In first quadrant, the above given curves intersect each other at (1, 2).
So, the required area =∫10((x+1)−2x)dx
=[x22+x−2xloge2]10[∵∫axdx=axlogea+C]
=[12+1−2loge2+1loge2]
=32−1loge2
|
Topper's Solved these Questions
- AREABOOK - IIT JEE PREVIOUS YEARCHAPTER - AREAEXERCISE - AREA USING INTEGRATION
55 Videos
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)
8 Videos
- BINOMIAL THEOREMBOOK - IIT JEE PREVIOUS YEARCHAPTER - BINOMIAL THEOREMEXERCISE - Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
8 Videos
Similar Questions
Knowledge Check
The area (in sq units) of the region bounded by the curve 2x=y2−1andx=0 is
A1/3B2/3C1D2The area (in sq unit) of the region enclosed by the curves y=x2andy=x3 is
A112B16C13D1The area bounded by the curves x+y=2 and y=x2 above x-axis in the first quadrant is ,
A12B23C1012D65
The area (in sq. units) bounded by the curves y=x (x−3)2 and y=x is
View SolutionThe area of the region, bounded by the curves y=sin−1x+x(1−x)andy=sin−1x−x(1−x) in the first quadrant (in sq. units), is
View SolutionThe area (in sq. units) of the region bounded by the curve 12y=36−x2 and the tangents drawn to it at the points, where the curve intersects the x-axis is
View SolutionThe area of the region bounded by the curves x=y2−2 and x=y is
View SolutionThe area (in sq. units) of the region bounded by the X-axis and the curve y=1−x−6x2 is
View Solution
