The area (in sq units) of the region bounded by the parabola, $y = x^{2} + 2$ and the lines, $y = x + 1, x = 0 and x = 3$ , is

A

$\frac{15}{2}$

B

$\frac{17}{4}$

C

$\frac{21}{2}$

D

$\frac{15}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Given equation of parabola is $y = x^{2} + 2,$ and the line is $y = x + 1$

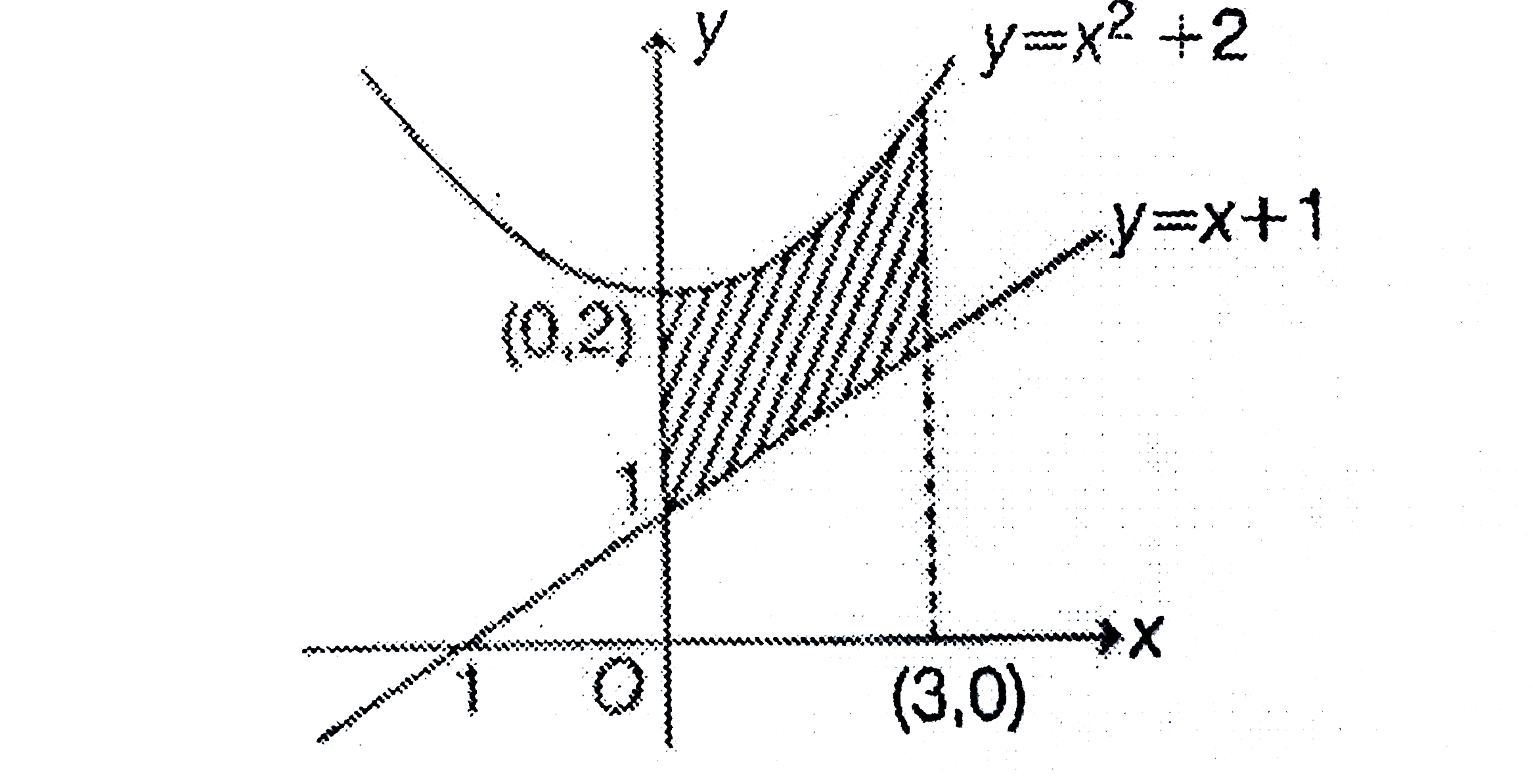
The required area = area of shaded region
$= \int_{0}^{3} ((x^{2} + 2) - (x + 1)) d x = \int_{0}^{3} (x^{2} - x + 1) d x$
$= {[\frac{x^{3}}{3} - \frac{x^{2}}{2} + x]}_{0}^{3} = (\frac{27}{3} - \frac{9}{2} + 3) - 0$
$= 9 - \frac{9}{2} + 3 = 12 - \frac{9}{2} = \frac{15}{2}$ sq units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the region bounded by the parabola $y = x^{2} + 2$ and the lines y = x, x = 0 and x = 3 is
A $\frac{7}{2} s q . u n i t s$
B $\frac{17}{2} s q . u n i t s$
C $\frac{21}{2} s q . u n i t s$
D $\frac{15}{2} s q . u n i t s$
Question 2 - Select One
The area of the region bounded by the parabola $y = x^{2}$ and the line y = 4x is
A $\frac{32}{3} s q . u n i t s$
B $\frac{16}{3} s q . u n i t s$
C $\frac{8}{3} s q . u n i t s$
D $\frac{4}{3} s q . u n i t s$
Question 3 - Select One
The area (in sq units) of the region bounded by the curve $2 x = y^{2} - 1 and x = 0$ is
A $1 / 3$
B $2 / 3$
C1
D2

IIT JEE PREVIOUS YEAR-AREA-AREA USING INTEGRATION

Home
Ask Doubt
Profile