Question

Compute the area of the region bounded by the curves $y=ex{\left(\log \right)}_{e}x$ and $y=\frac{\log x}{ex}$

Answer

`((e^(2)-5)/(4e))` sq units

Explanation

Both the curves are defined for `x gt 0`
Both are positive when ` x gt 1` and negative when ` 0 lt x lt 1.`
We know that, `lim_(x to 0^(+))(logx) to -oo`
Hence, `lim_(x to 0^(+))(logx)/(ex) to -oo,` Thus, Y-axis is asymptote of second curve.
And `lim_(x to 0^(+))ex logx " "[(0) xx oo " form"]`
`=lim_(x to 0^(+))(elogx)/(1//x) " "[-(oo)/(oo) " form"]`
`=lim_(x to 0^(+))(e((1)/(x)))/((-(1)/(x^(2))))=0 " " `[using L'Hospital's rule]
Thus, the first curves starts from (0, 0) but does not include (0, 0).
Now, the given curves intersect, therefore
`ex logx = (logx)/(ex)`
i.e. `(e^(2)x^(2)-1)logx=0`
` rArr x=1,(1)/(e) " "[ because x gt 0]`

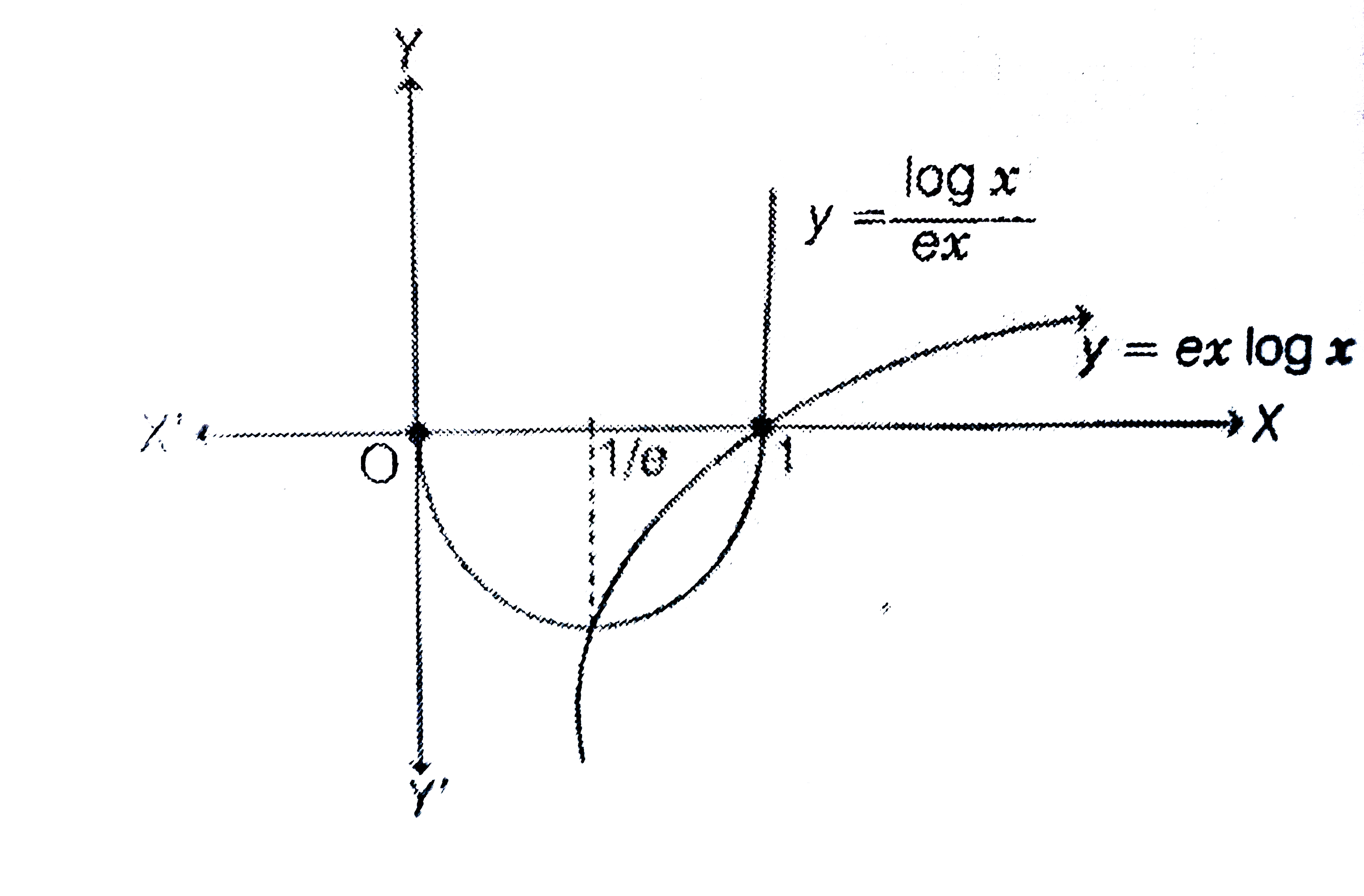
`therefore ` The required area
`=int_(1//e)^(1) (((logx))/(ex) -ex logx)dx`
`=(1)/(e) [ ((logx)^(2))/(2)]_(1//e)^(1) -e[(x^(2))/(4) (2logx-1)]_(1//e)^(1) = ((e^(2)-5)/(4e))` sq units