A curve $C$ passes through (2,0) and the slope at $(x, y)$ as $\frac{{(x + 1)}^{2} + (y - 3)}{x + 1} .$ Find the equation of the curve. Find the area bounded by curve and x-axis in the fourth quadrant.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $y = x^{2} - 2 x, \frac{4}{3}$ sq units

Here, slope of tangent,
$\frac{d y}{d x} = \frac{{(x + 1)}^{2} + (y - 3)}{(x + 1)}$
$\Rightarrow \frac{d y}{d x} = (x + 1) + \frac{(y - 3)}{(x + 1)},$
Put $x + 1 = X and y - 3 = Y$
$\Rightarrow \frac{d y}{d x} = \frac{d Y}{d X}$
$∴ \frac{d Y}{d X} = X + \frac{Y}{X}$
$\Rightarrow \frac{d Y}{d X} - \frac{1}{X} Y = X$
IF $= e^{\int - \frac{1}{X} d x} = e^{- log X} = \frac{1}{X}$
$∴ Solution is, Y = \cdot \frac{1}{X} = \int X \cdot \frac{1}{X} d x + c$
$\Rightarrow \frac{Y}{X} = X + c$

$y - 3 = {(x + 1)}^{2} + c (x + 1),$ which passes through (2, 0).
$\Rightarrow - 3 = {(3)}^{2} + 3 c$
$\Rightarrow c = - 4$
$∴$ Required curve
$y = {(x + 1)}^{2} - 4 (x + 1) + 3$
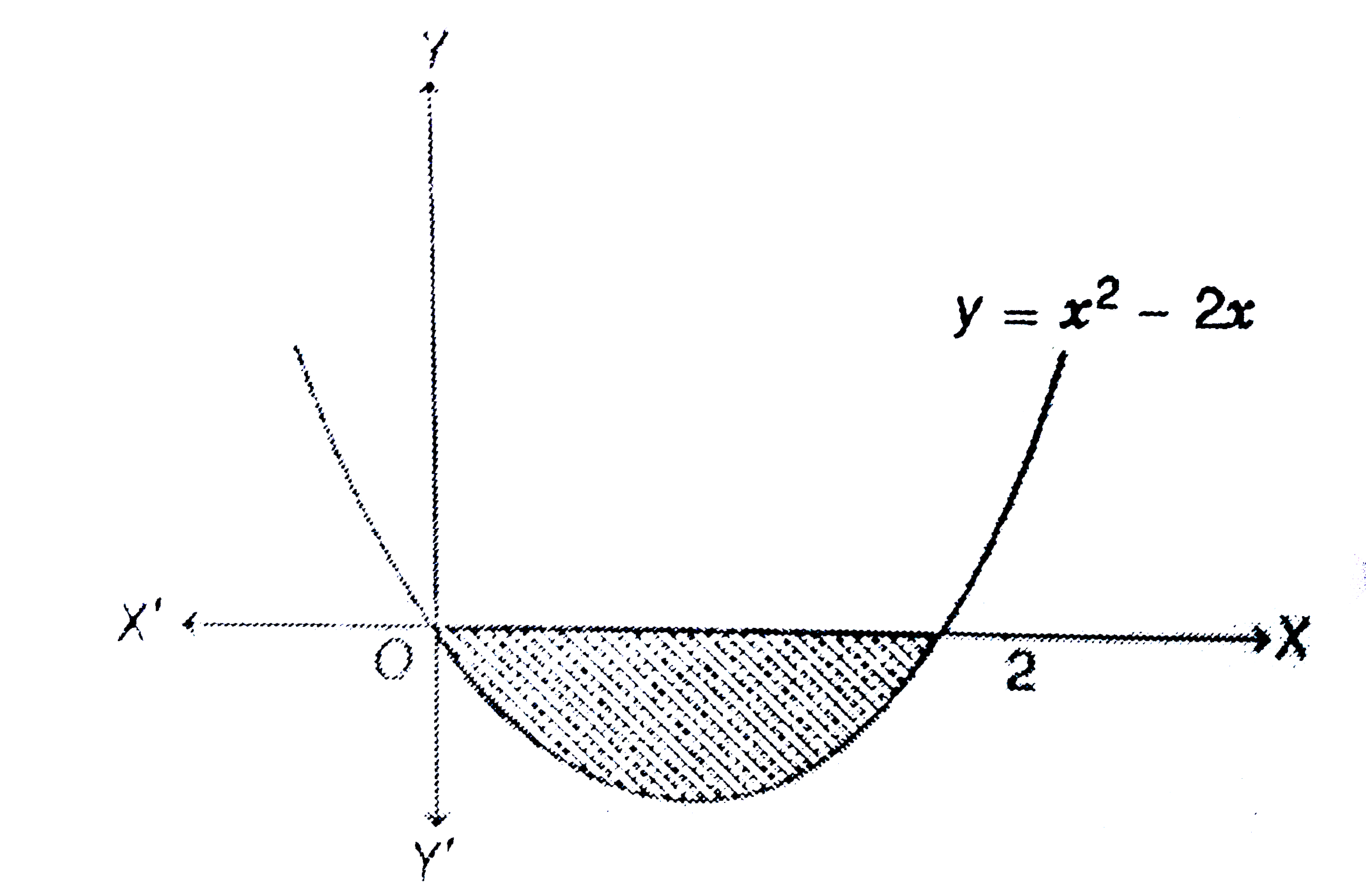
$\Rightarrow y = x^{2} - 2 x$
$∴ Required area = ∣ ∣ ∣ \int_{0}^{2} (x^{2} - 2 x) d x ∣ ∣ ∣ = ∣ ∣ ∣ ∣ {(\frac{x^{3}}{3} - x^{2})}_{0}^{2} ∣ ∣ ∣ ∣$
$= \frac{8}{3} - 4 = \frac{4}{3}$ sq units

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area bounded by the curve $y = x (x^{2} - 1)$ and x-axis is
A0
B $\frac{1}{2}$
C1
D $\frac{1}{4}$

IIT JEE PREVIOUS YEAR-AREA-AREA USING INTEGRATION

Home
Ask Doubt
Profile