Twenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is:
12.5
10
25
30
The correct Answer is:C
Total length =2r+rθ=20
⇒θ=20−2rr
Now, are of flower-bed,
A=12r2θ
⇒A12r2(20−2rr)
⇒A=10r−r2
∴dAdr=10−2r
For maximum or minima, put, dAdr=0
⇒10−2r=0⇒r=5
∴Amax=12(5)2[20−2(5)5]
=12×25×2=25 sq. m
Topper's Solved these Questions
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA (OBJECTIVE QUESTIONS II)
8 Videos
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA (MATCH THE COLUMNS)
1 Videos
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - ROLLES AND LAGRANGES THEOREM (ANALYTICAL & DESCRIPTIVE QUESTION)
1 Videos
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Integer Answer Type Question)
1 Videos
- AREABOOK - IIT JEE PREVIOUS YEARCHAPTER - AREAEXERCISE - AREA USING INTEGRATION
55 Videos
Similar Questions
Knowledge Check
Twenty meters of wire is available for fencing a flower -bed in the form of a circular sector .Then the maximum area in square meters of the flower bed is
A12.5B10C25D30
Find the area of the flower bed (with semicircular ends).

View SolutionFind the area of the flower bed (with semi-circular ends) shown in figure.

View SolutionFind the area of the flower bed (with semi-circular ends) shown in figure

View SolutionIn each of the corners, there is a flower bed in the form of a quadrant of a circle of radius 2 m. Also, there is a flower bed in the form of a circle of radius 2 m in the middle of the plot. Find the area of the remaining plot.

View SolutionThere are two circular flower beds on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
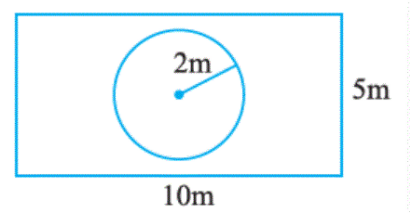
View SolutionThe adjoining figure represents a rectangular lawn with a circular flower bed in the middle. Find:
(i) the area of the whole land
(ii) the area of the flower bed
(iii) the area of the lawn excluding the area of the flower bed
(iv) the circumference of the flower bed.
View SolutionIn Figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawns and the flower beds.
View Solution

