Question

A line L : y = mx + 3 meets y-axis at E (0, 3) and the arc of the parabola $y^2=16x$ $0\le y\le 6$ at the point art $F(x_0,y_0)$. The tangent to the parabola at $F(X_0,Y_0)$ intersects the y-axis at $G(0,y)$. The slope m of the line L is chosen such that the area of the triangle EFG has a local maximum P) m= Q) = Maximum area of $△EFG$ is (R) $y_0=$ (S) $y_1=$

Options

A. `{:(P,, Q,, R,, S), (4,, 1,, 2,, 3):}`
B. `{:(P,, Q,, R,, S), (3,, 4,, 1,, 2):}`
C. `{:(P,, Q,, R,, S), (1,, 3,, 2,, 4):}`
D. `{:(P,, Q,, R,, S), (1,, 3,, 4,, 2):}`

Answer

A::B::C::D

Explanation

Here, `y ^(2) = 16x, 0 le y le 6`

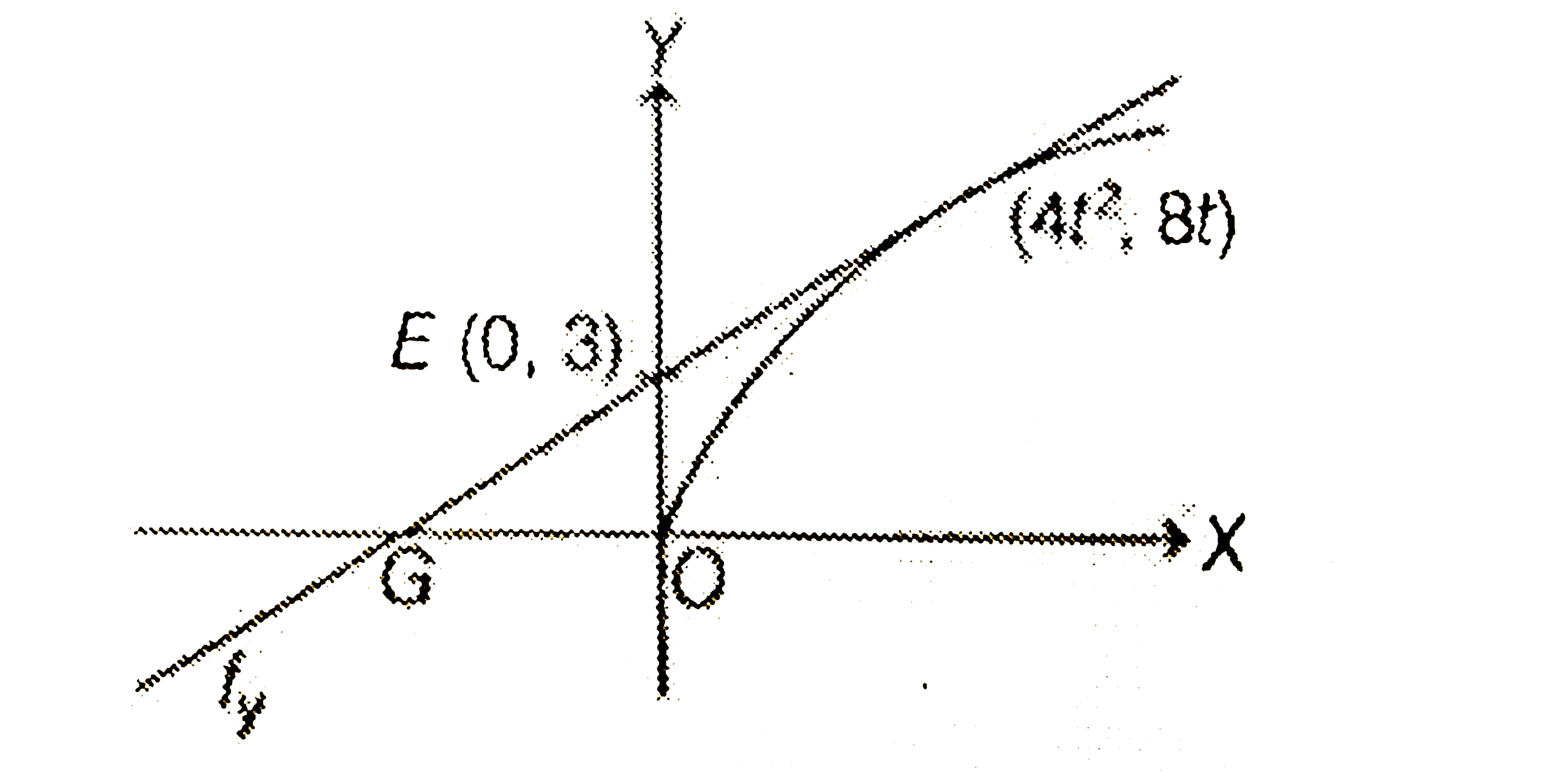
Tangent at `F, y t = x + at ^(2)`
At `" " x = 0, y = at = 4t`
Also, ` ( 4 t ^(2), 8 t) ` satisfy `y = mx + c `
`rArr " " 8t k= 4m t ^(2) + 3 `
`rArr " " 4 mt^(2) - 8 t + 3 = 0`
`therefore" "` Area of ` Delta = (1)/(2) |{:( 0,, 3,,1 ), ( 0,, 4t,, 1), (4t^(2),, 8t,, 1):}| = (1)/(2) * 4t^(2)( 3- 4t)`
`" " A = 2 [ 3t^(2) - 4t^(3) ]`
`therefore " " ( dA)/( dt) = 2 [ 6t - 12 t ^(2)] = - 12 t (12 t - 1)`
` (##41Y_SP_MATH_C10_E04_038_S02##) `
`therefore ` Maximum at ` t = (1)/(2) and 4 mt ^(2) - 8t + 3 =0`
`rArr m - 4 + 3 = 0`
`rArr " " m = 1 `
`" " G(0, 4t) rArr G (0, 2)`
`rArr " " y _1= 2 `
`(x _0, y _0) = ( 4t^(2) , 8t) = ( 1, 4)`
`" " y _0 = 4 `
`therefore" " ` Area` = 2((3)/(4) - (1)/(2)) = (1)/(2)`