Question

The total number of local maxima and local minima of the function $f\left(x\right)=$$\{\begin{array}{c}{(2+x)}^3;-3<x\le -1\\ x^{\frac{2}{3}};-1<x<2\end{array}$ is

Options

A. 0
B. 1
C. 2
D. 3

Answer

C

Explanation

Given `f(x)={{:((2+x)^(3),if -3 lt x le-1),(x^(2//3), if -1 lt x lt2):}`
`rArr f'(x)={{:(3(x+2)^(2),if -3 lt x le-1),((2)/(3)x^(1/3), if -1 lt x lt2):}`

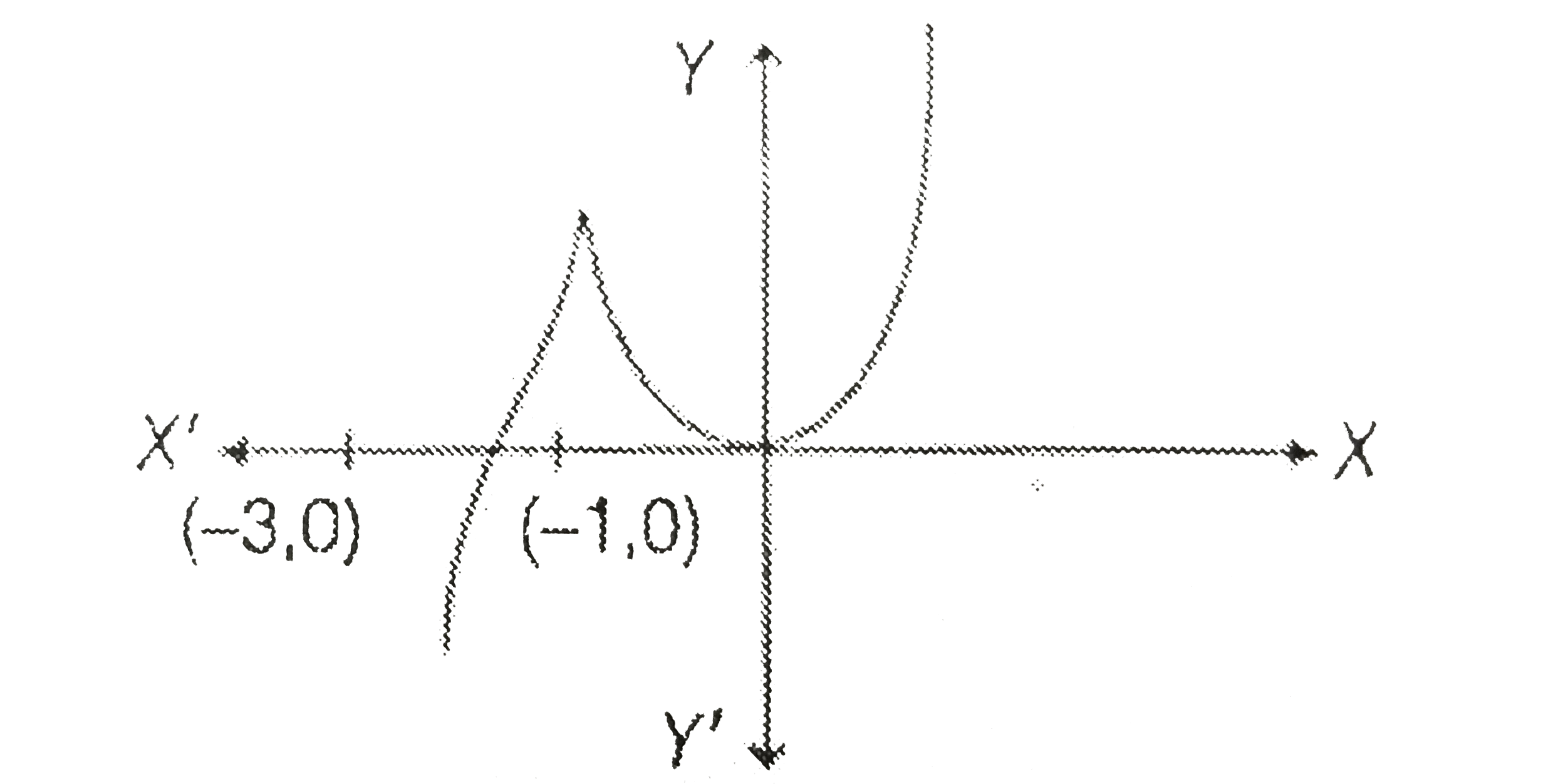
Clearly, f'(x) changes is sign at x=-1 from + ve to -ve and so f(x) has local maxima at x=-1.
Also, f'(0) does not exist but `f'(0^(-)) lt 0 and f'(0^(+))lt0`.
It can only be inferred that f(x) has a possibuility of a minima at x=0 . Hence, the given function has one local maxima at x=-1 adn one loca minima at x=0.